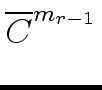

Next: Bibliography
Up: Modular Computation
Previous: Modular computation of the determinant
We conclude this chapter with another modular algorithm.
We assume that we have a highly efficient matrix multiplication
over
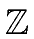 /p
/p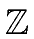 mathend000#, for any machine-word size prime number p
mathend000#,
and would like to take advantage of it for multipying
matrcies with integer coefficients.
This can be achieved by means of a modular algorithm,
based on the Chinese Remaindering Algorithm.
mathend000#, for any machine-word size prime number p
mathend000#,
and would like to take advantage of it for multipying
matrcies with integer coefficients.
This can be achieved by means of a modular algorithm,
based on the Chinese Remaindering Algorithm.
Consider two square matrices
A = (ai, j, 1  i
i  j
j  n)
mathend000#
and
B = (bi, j, 1
n)
mathend000#
and
B = (bi, j, 1  i
i  j
j  n)
mathend000# of order n
mathend000# with coefficients in
n)
mathend000# of order n
mathend000# with coefficients in
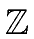 mathend000#.
Let
|| A||
mathend000#.
Let
|| A||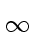 mathend000# and
|| B||
mathend000# and
|| B||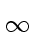 mathend000# be the maximum absolute value
of a coefficient in A
mathend000# and B
mathend000#, respectively.
Let
C = (ci, j, 1
mathend000# be the maximum absolute value
of a coefficient in A
mathend000# and B
mathend000#, respectively.
Let
C = (ci, j, 1  i
i  j
j  n)
mathend000# be the matrix product
AB
mathend000# and let m > 2
mathend000# be any odd integer (prime or not).
For all
1
n)
mathend000# be the matrix product
AB
mathend000# and let m > 2
mathend000# be any odd integer (prime or not).
For all
1  i
i  j
j  n
mathend000#, we have
n
mathend000#, we have
ci, j = 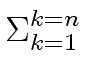 ai, kbk, j, ai, kbk, j, |
(137) |
and thus
ci, j  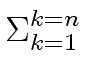 ai, kbk, jmod m. ai, kbk, jmod m. |
(138) |
Now, let
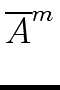 = (
= (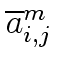 , 1
, 1  i
i  j
j  n)
mathend000#
and
n)
mathend000#
and
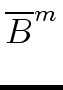 = (
= (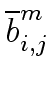 , 1
, 1  i
i  j
j  n)
mathend000#
be the images of A
mathend000# and B
mathend000# modulo m
mathend000#. (Hence the coefficient
n)
mathend000#
be the images of A
mathend000# and B
mathend000# modulo m
mathend000#. (Hence the coefficient
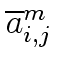 mathend000# of
mathend000# of
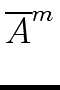 mathend000# is the remainder of ai, j
mathend000# modulo m
mathend000#.)
Let
mathend000# is the remainder of ai, j
mathend000# modulo m
mathend000#.)
Let
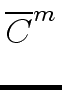 = (
= (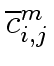 , 1
, 1  i
i  j
j  n)
mathend000#
be the matrix product
n)
mathend000#
be the matrix product
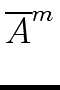
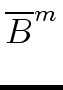 mathend000#
computed in
mathend000#
computed in
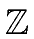 /m
/m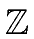 mathend000#.
Hence, we have
mathend000#.
Hence, we have
Combining the relations
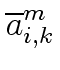 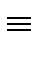 ai, kmod m and ai, kmod m and 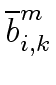 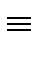 bi, kmod m bi, kmod m |
(140) |
with Equations (138) and (139)
we obtain
ci, j 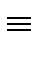 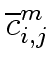 mod m. mod m. |
(141) |
In particular, if we use a symmetric representation
- 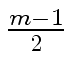 ...
... 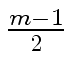 mathend000#
for representing the elements of
mathend000#
for representing the elements of
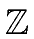 /m
/m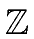 mathend000# and if we have
| ci, j| <
mathend000# and if we have
| ci, j| < 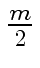 mathend000#, then Equation (141)
simply becomes
ci, j =
mathend000#, then Equation (141)
simply becomes
ci, j = 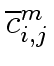 mathend000#.
mathend000#.
Observe that for all
1  i
i  j
j  n
mathend000#, we have
n
mathend000#, we have
| ci, j | 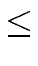 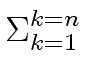 | ai, k | | bk, j | | ai, k | | bk, j | 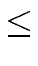 n | | A | n | | A | 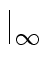 | | B | | | B | 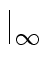 . . |
(142) |
Hence we define
M = n|| A||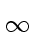 || B||
|| B||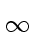 mathend000#.
We are ready to state a modular algorithm.
mathend000#.
We are ready to state a modular algorithm.
Algorithm 6
![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $A=(a_{ij...
... := $c_{i,j} - m$\ \\
\> {\bf return}($(c_{ij})$)
\end{tabbing}\end{minipage}}](img216.png) mathend000#
mathend000#
Note that the first for loop computes the matrcies
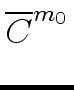 ,...,
,...,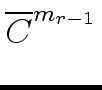 mathend000#
by the classical method.
However, one can use instead any other algorithm (like Strassen's)
computing these matrices.
Let us give an upper bound for the number of machine-word operations
required by Algorithm 6.
It suffices to estimate each of the two for loops.
The first one runs in O(rn3)
mathend000# and the second one in
O(n2r2)
mathend000#.
This is a better estimate than the one which can be given
for the naive (non-modular approach):
O(n3r2)
mathend000#.
mathend000#
by the classical method.
However, one can use instead any other algorithm (like Strassen's)
computing these matrices.
Let us give an upper bound for the number of machine-word operations
required by Algorithm 6.
It suffices to estimate each of the two for loops.
The first one runs in O(rn3)
mathend000# and the second one in
O(n2r2)
mathend000#.
This is a better estimate than the one which can be given
for the naive (non-modular approach):
O(n3r2)
mathend000#.


Next: Bibliography
Up: Modular Computation
Previous: Modular computation of the determinant
Marc Moreno Maza
2007-01-10
![]() i
i ![]() j
j ![]() n)
n)
![]() i
i ![]() j
j ![]() n)
n)
![]()
![]()
![]()
![]() i
i ![]() j
j ![]() n)
n)
![]() i
i ![]() j
j ![]() n
n
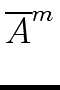 = (
= (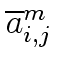 , 1
, 1 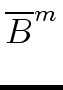 = (
= (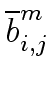 , 1
, 1 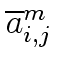
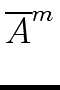
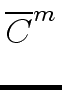 = (
= (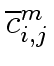 , 1
, 1 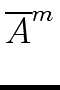
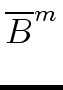
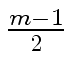 ...
... 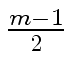
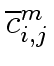
![]() i
i ![]() j
j ![]() n
n
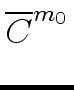 ,...,
,...,