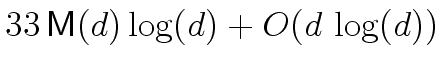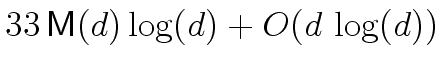
Next: Bibliography
Up: Division with remainder using Newton
Previous: Division with remainder using Newton
In this section, we assume that R
mathend000# is a field.
Algorithm 6 has the same specifications
as the EEA and runs in
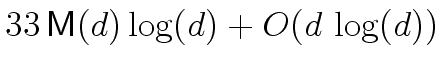mathend000# operations
(+ , x , ÷ )
mathend000# in R
mathend000#
for input polynomials in degree d
mathend000#.
The key algorithm is Algorithm 4, called the Half-GCD
algorithm.
This algorithm originated in the ideas of Lehmer, Knuth and Schönhage.
Though, it has appeared in many books including [AA74,Yap93,GG99] and in many other publications, it is frequently specified incorrectly. This creates an implementation challenge. We adapted Yap's [Yap93]
Algorithm 4
![\fbox{
\begin{minipage}{12 cm}
\begin{description}
\item[{\sc Input:}] $a,\, b\,...
...{\sc 17} \> \> \mbox{{\bf return}} $M_3 M_2 M_1$\
\end{tabbing}\end{minipage}}](img67.png)
mathend000#
Algorithm 5
![\fbox{
\begin{minipage}{12 cm}
\begin{description}
\item[{\sc Input:}] $a,\, b\,...
... 10} \> \> \mbox{{\bf return}} $M_3\, M_2\, M_1$\
\end{tabbing}\end{minipage}}](img68.png)
mathend000#
Algorithm 6
![\fbox{
\begin{minipage}{12 cm}
\begin{description}
\item[{\sc Input:}] $a,\, b\,...
...> \> \mbox{{\bf else return}} {\rm FEEA}$(b,a)$\\
\end{tabbing}\end{minipage}}](img69.png)
mathend000#
Next: Bibliography
Up: Division with remainder using Newton
Previous: Division with remainder using Newton
Marc Moreno Maza
2007-01-10