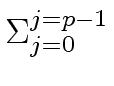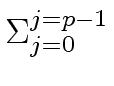

Next: Implementing Computer Algebra: basic ideas
Up: A review of complexity notions
Previous: Orders of magnitude
DIVIDE-AND-CONQUER ALGORITHMS proceed as follows.
- Divide
- the input problem into sub-problems.
- Conquer
- on the sub-problems by solving them directly if they are small
enough or proceed recursively.
- Combine
- the solutions of the sub-problems to obtain the solution of the
input problem.
EQUATION SATISFIED BY T(N)
MATHEND000#.
Assume that the size of the input problem increases with an integer n
mathend000#.
Let T(n)
mathend000# be the time complexity of a divide-and-conquer algorithm
to solve this problem.
Then T(n)
mathend000# satisfies an equation of the form:
| T(n) = a T(n/b) + f (n). |
(14) |
where
f (n)
mathend000# is the cost of the combine-part, a 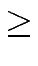 1
mathend000# is the
number of recursively calls and n/b
mathend000# with b > 1
mathend000#
is the size of a sub-problem.
1
mathend000# is the
number of recursively calls and n/b
mathend000# with b > 1
mathend000#
is the size of a sub-problem.
LABELED TREE ASSOCIATED WITH THE EQUATION.
Assume n
mathend000# is a power of b
mathend000#, say n = bp.
mathend000#
To solve this equation we can associate a labeled tree
 (n)
mathend000# to it
as follows.
(n)
mathend000# to it
as follows.
- (1)
mathend000#
- If n = 1
mathend000#, then
 (n)
mathend000# is reduced to a single leaf by labeled T(1)
mathend000#.
(n)
mathend000# is reduced to a single leaf by labeled T(1)
mathend000#.
- (2)
mathend000#
- If n > 1
mathend000#, then the root of
 (n)
mathend000# is labeled
by f (n)
mathend000# and
(n)
mathend000# is labeled
by f (n)
mathend000# and
 (n)
mathend000# possesses
a
mathend000# labeled sub-trees all equal to
(n)
mathend000# possesses
a
mathend000# labeled sub-trees all equal to
 (n/b)
mathend000#.
(n/b)
mathend000#.
The labeled tree
 (n)
mathend000# associated with
T(n) = a T(n/b) + f (n)
mathend000#
has height p + 1
mathend000#.
Moreover the sum of its labels is T(n)
mathend000#.
(n)
mathend000# associated with
T(n) = a T(n/b) + f (n)
mathend000#
has height p + 1
mathend000#.
Moreover the sum of its labels is T(n)
mathend000#.
LET US GIVE TWO EXAMPLES.
- Consider the relation:
| T(n) = 2 T(n/2) + n2. |
(15) |
We obtain:
T(n) = n2 + 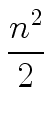 + + 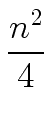 + + 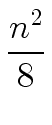 + ... + + ... + 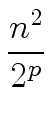 + n T(1). + n T(1). |
(16) |
Hence we have:
T(n) 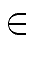  (n2). (n2). |
(17) |
- Consider the relation:
We obtain:
T(n) 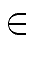  (log3(n)n). (log3(n)n). |
(19) |
A FORMULA TO ESTIMATE T(N)
MATHEND000#.
Let a > 0
mathend000# be an integer and let
S, T : 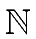
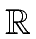 +
mathend000# be functions
such that
+
mathend000# be functions
such that
- (i)
mathend000#
-
S(2 n)
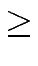 2 S(n)
mathend000# and
S(n)
2 S(n)
mathend000# and
S(n) 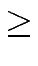 n
mathend000#.
n
mathend000#.
- (ii)
mathend000#
- If n = 2p
mathend000# then
T(n)
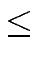 a T(n/2) + S(n).
mathend000#
a T(n/2) + S(n).
mathend000#
Then for n = 2p
mathend000# we have
- (1)
mathend000#
- if a = 1
mathend000# then
T(n) 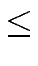 (2 - 2/n) S(n) + T(1) (2 - 2/n) S(n) + T(1) 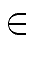  (S(n)), (S(n)), |
(20) |
- (2)
mathend000#
- if a = 2
mathend000# then
T(n) 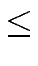 S(n) log2(n) + T(1) n S(n) log2(n) + T(1) n 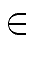 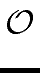 (log2(n) S(n)), (log2(n) S(n)), |
(21) |
- (3)
mathend000#
- if a
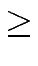 3
mathend000# then
3
mathend000# then
T(n) 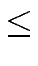 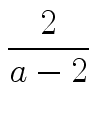 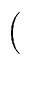 nlog2(a)-1 - 1 nlog2(a)-1 - 1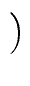 S(n) + T(1) nlog2(a) S(n) + T(1) nlog2(a)   (S(n) nlog2(a)-1). (S(n) nlog2(a)-1). |
(22) |
Indeed
| T(2p) |
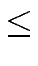 |
a T(2p-1) + S(2p) |
| |
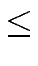 |
a a T(2p-2) + S(2p-1) a T(2p-2) + S(2p-1)![$\displaystyle \left.\vphantom{ a \, T(2^{p-2}) + S(2^{p-1}) }\right]$](img288.png) + S(2p) + S(2p) |
| |
= |
a2 T(2p-2) + a S(2p-1) + S(2p) |
| |
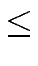 |
a2 a T(2p-3) + S(2p-2) a T(2p-3) + S(2p-2)![$\displaystyle \left.\vphantom{ a \, T(2^{p-3}) + S(2^{p-2}) }\right]$](img290.png) + a S(2p-1) + S(2p) + a S(2p-1) + S(2p) |
| |
= |
a3 T(2p-3) + a2 S(2p-2) + a S(2p-1) + S(2p) |
| |
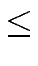 |
ap T(1) + 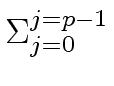 aj S(2p-j) aj S(2p-j) |
|
(23) |
Moreover
| S(2p) |
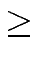 |
2 S(2p-1) |
| S(2p) |
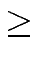 |
22 S(2p-2) |
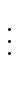 |
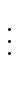 |
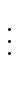 |
| S(2p) |
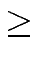 |
2j S(2p-j) |
|
(24) |
Thus
Hence
T(2p) 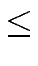 ap T(1) + S(2p) ap T(1) + S(2p) 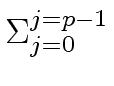 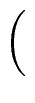 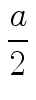 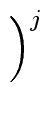 . . |
(26) |
For a = 1
mathend000# we obtain
| T(2p) |
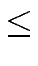 |
T(1) + S(2p) 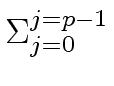  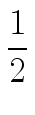  |
| |
= |
T(1) + S(2p) 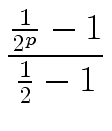 |
| |
= |
T(1) + S(n) (2 - 2/n). |
|
(27) |
For a = 2
mathend000# we obtain
| T(2p) |
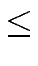 |
2p T(1) + S(2p) p |
| |
= |
n T(1) + S(n) log2(n). |
|
(28) |


Next: Implementing Computer Algebra: basic ideas
Up: A review of complexity notions
Previous: Orders of magnitude
Marc Moreno Maza
2007-01-10
![]() (n)
(n)
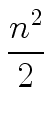 +
+ 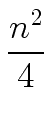 +
+ 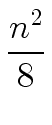 + ... +
+ ... + 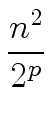 + n T(1).
+ n T(1).![]()
![]()
![]() +
+
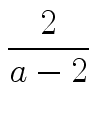
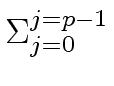 aj S(2p-j)
aj S(2p-j)