![\begin{figure}\htmlimage[no_transparent]
\centering
\includegraphics[scale=0.5]{uma2add.eps}
\end{figure}](img9.png) |
We iluustrate below the gap between naive and optimized implementations of the same algorithm.
Next, we show benchmarks between classical and FFT-based univariate polynomial multiplication.
The maple work sheet Bareiss.mw iluustrates the problem of intermediate expression swell. In many situations, this problem is solved by means of modular methods. Here's an example of such method that will study in detail later

Another example of intermediate expression swell is given below. Consider the polynomials
| r0 = x |
(1) |
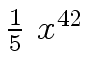 +
+ 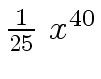 -
- 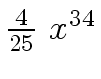 +
+ 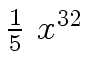 +
+ 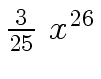 -
- 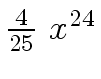 -
- 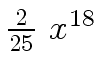 -
- 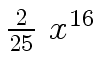 +
+ 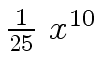 -
- 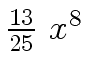 -
- 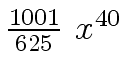 -
- 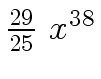 +
+ 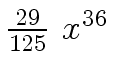 -
- 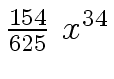 -
- 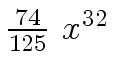 +
+ 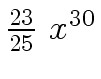 -
- 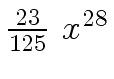 +
+ 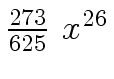 +
+ 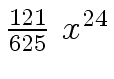 +
+ 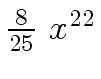 -
- 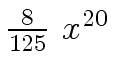 -
- 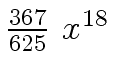 +
+ 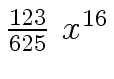 +
+ 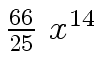 -
- 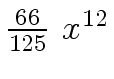 +
+ 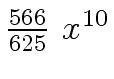 -
- 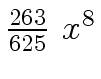 + x
+ x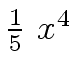 +
+ 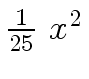 +
+ 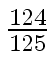
 +
+ 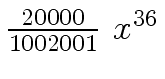 -
- 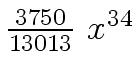 +
+ 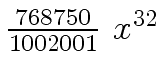 -
- 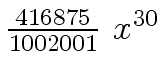 -
- 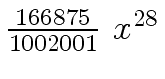 +
+ 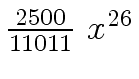 -
- 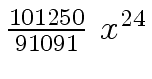 -
- 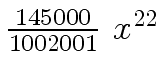 +
+ 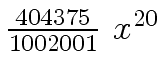 -
- 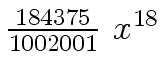 -
- 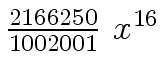 -
- 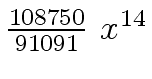 -
- 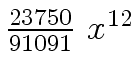 -
- 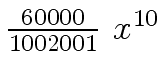 -
- 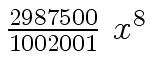 -
- 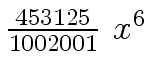 +
+ 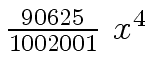 -
- 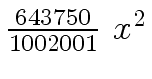 -
- 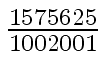
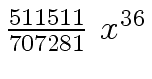 -
- 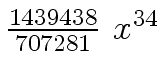 +
+ 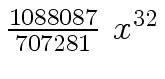 +
+ 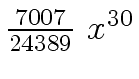 -
- 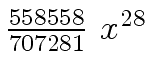 +
+ 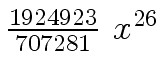 -
- 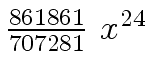 -
- 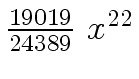 +
+ 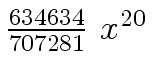 +
+ 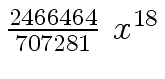 -
- 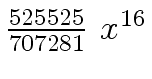 +
+ 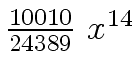 -
- 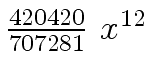 +
+ 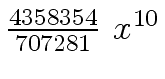 -
- 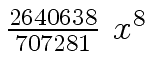 -
- 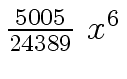 +
+ 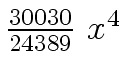 +
+ 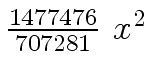 -
- 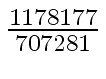
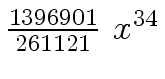 -
- 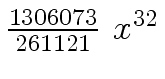 -
- 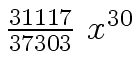 -
- 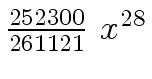 -
- 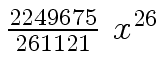 +
+ 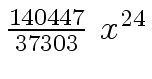 +
+ 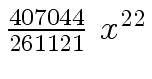 -
- 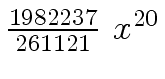 -
- 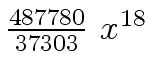 -
- 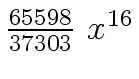 -
- 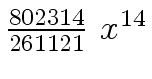 -
- 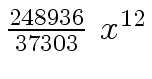 -
- 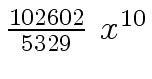 +
+ 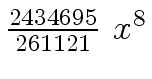 -
- 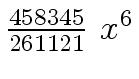 -
- 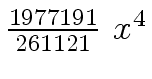 -
- 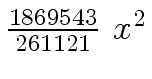 +
+ 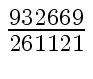
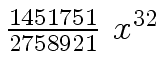 +
+ 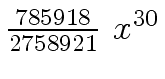 +
+ 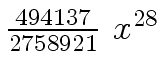 +
+ 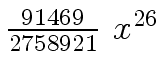 -
- 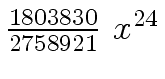 +
+ 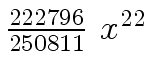 +
+ 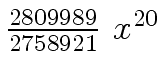 +
+ 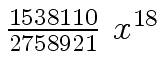 -
- 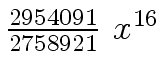 +
+ 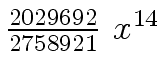 +
+ 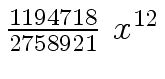 +
+ 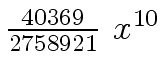 -
- 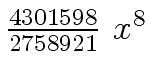 +
+ 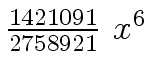 +
+ 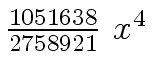 -
- 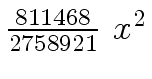 -
- 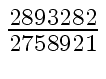
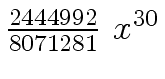 +
+ 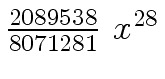 -
- 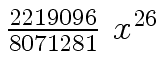 -
- 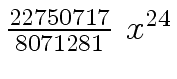 +
+ 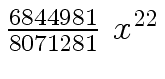 +
+ 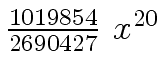 +
+ 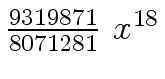 -
- 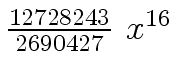 +
+ 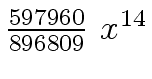 -
- 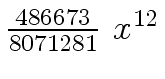 -
- 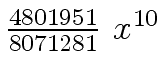 -
- 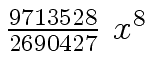 +
+ 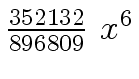 +
+ 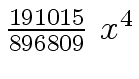 -
- 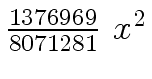 -
- 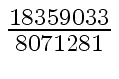
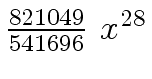 +
+ 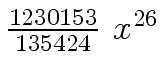 -
- 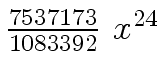 +
+ 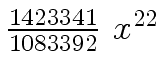 -
- 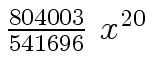 +
+ 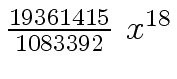 -
- 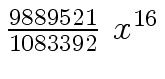 +
+ 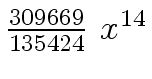 +
+ 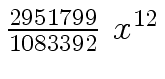 +
+ 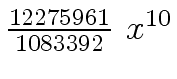 -
- 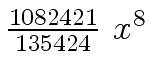 +
+ 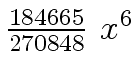 +
+ 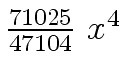 +
+ 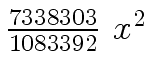 -
- 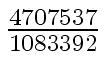
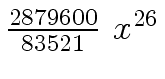 -
- 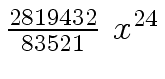 +
+ 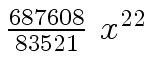 -
- 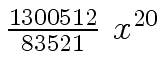 +
+ 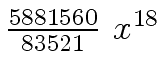 -
- 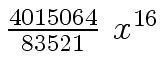 +
+ 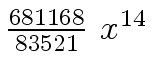 +
+ 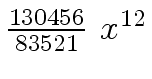 +
+ 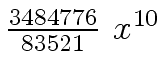 -
- 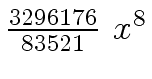 +
+ 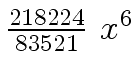 +
+ 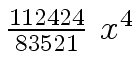 +
+ 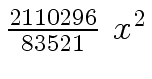 -
- 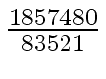
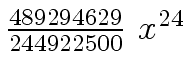 -
- 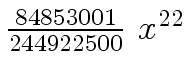 +
+ 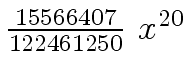 -
- 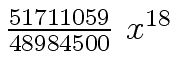 +
+ 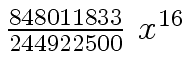 -
- 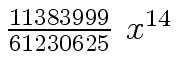 +
+ 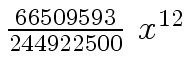 +
+ 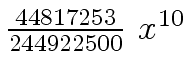 +
+ 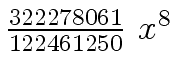 -
- 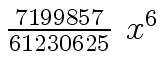 -
- 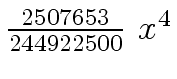 +
+ 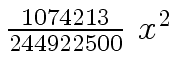 +
+ 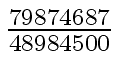
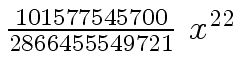 +
+ 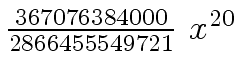 -
- 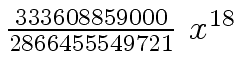 +
+ 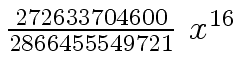 +
+ 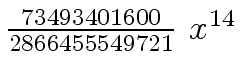 +
+ 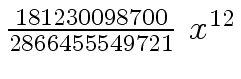 -
- 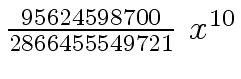 -
- 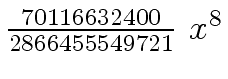 +
+ 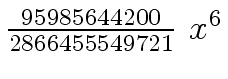 +
+ 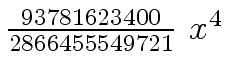 -
- 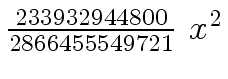 +
+ 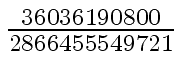
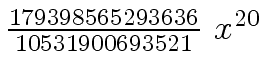 -
- 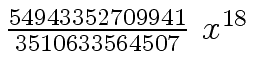 +
+ 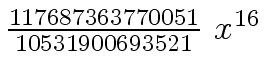 +
+ 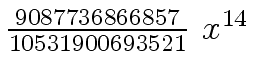 +
+ 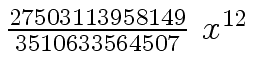 -
- 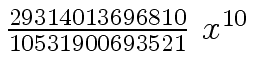 -
- 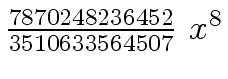 +
+ 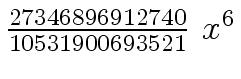 +
+ 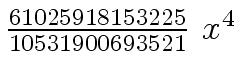 -
- 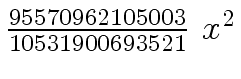 +
+ 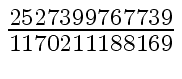
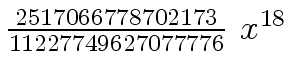 -
- 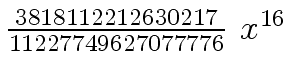 +
+ 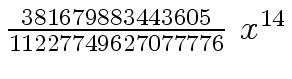 -
- 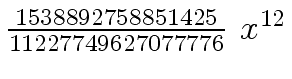 -
- 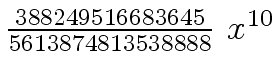 -
- 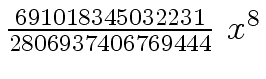 -
- 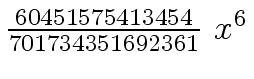 -
- 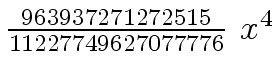 -
- 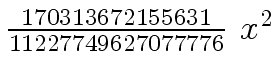 -
- 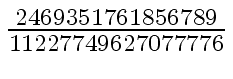
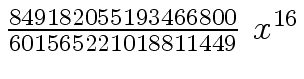 +
+ 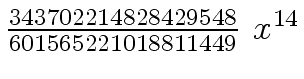 +
+ 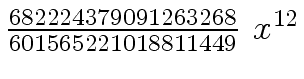 +
+ 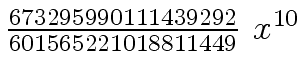 +
+ 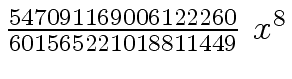 +
+ 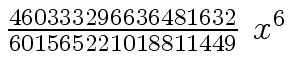 +
+ 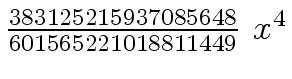 +
+ 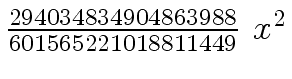 +
+ 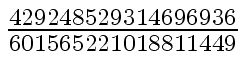
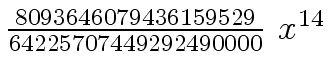 +
+ 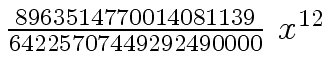 +
+ 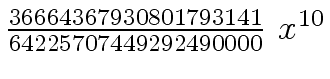 -
- 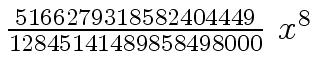 +
+ 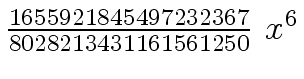 +
+ 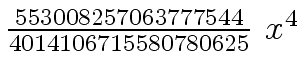 +
+ 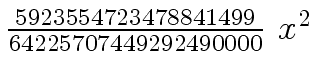 -
- 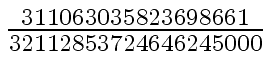
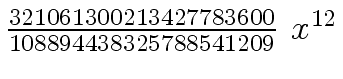 +
+ 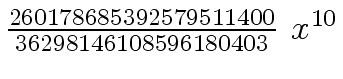 -
- 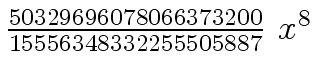 +
+ 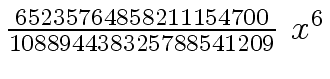 +
+ 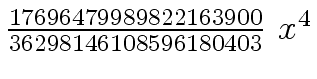 +
+ 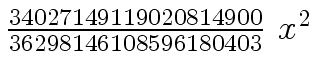 +
+ 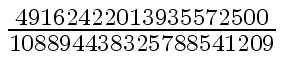
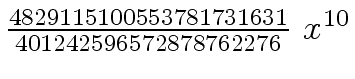 -
- 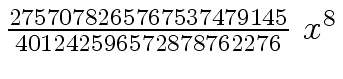 +
+ 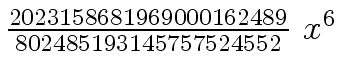 +
+ 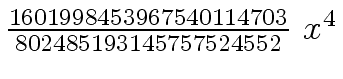 +
+ 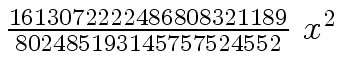 +
+ 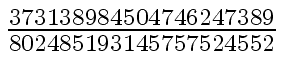
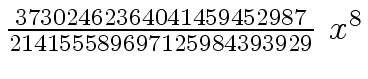 +
+ 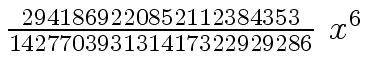 -
- 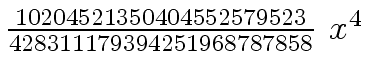 -
- 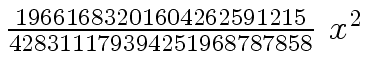 -
- 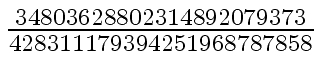
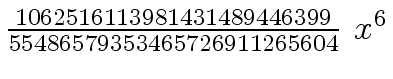 -
- 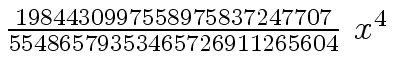 -
- 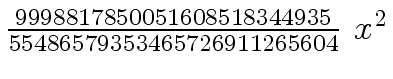 +
+ 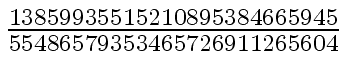
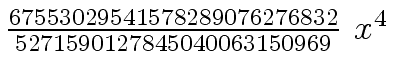 +
+ 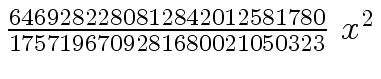 -
- 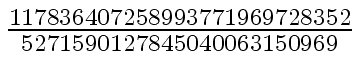
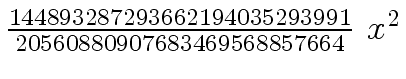 +
+ 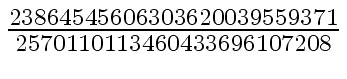
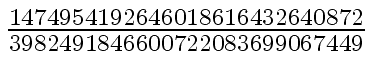
We will study modular methods for the Euclidean Algorithm too.