Next: Modular Gcd Algorithms in Up: Advanced Computer Algebra: The resultant Previous: Lucky and unlucky modular reductions
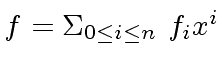 be a univariate
polynomial over
be a univariate
polynomial over
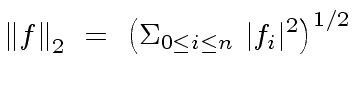 |
(72) |
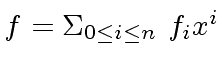 we shall compute a bound
we shall compute a bound ![$ h \in {\mbox{${\mathbb{C}}$}}[x]$](img265.png) we have
we have
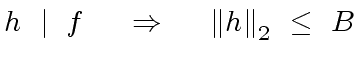 |
(73) |
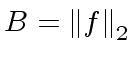 would work.
Unfortunately there are some counter-examples.
Though they are very rare, there are infinitely many of them.
would work.
Unfortunately there are some counter-examples.
Though they are very rare, there are infinitely many of them.
(2) -> factor(x^105 - 1)
(2)
2 4 3 2
(x - 1)(x + x + 1)(x + x + x + x + 1)
*
6 5 4 3 2
(x + x + x + x + x + x + 1)
*
8 7 5 4 3
(x - x + x - x + x - x + 1)
*
12 11 9 8 6 4 3
(x - x + x - x + x - x + x - x + 1)
*
24 23 19 18 17 16 14 13
x - x + x - x + x - x + x - x
12 11 10 8 7 6 5
+ x - x + x - x + x - x + x - x + 1
*
48 47 46 43 42 41 40
x + x + x - x - x - 2x - x
39 36 35 34 33
- x + x + x + x + x
32 31 28 26 24 22 20
+ x + x - x - x - x - x - x
17 16 15 14 13
+ x + x + x + x + x
12 9 8 7 6 5 2
+ x - x - x - 2x - x - x + x + x + 1
Type: Factored Polynomial Integer
Worse than that: for every 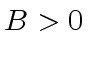 there exist infinitely many
there exist infinitely many 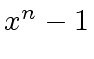 and satisfying
and satisfying
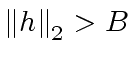 .
See [GG99] for more details.
.
See [GG99] for more details.
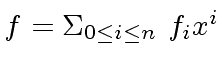 and define
and define
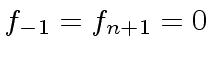 .
We calculate
.
We calculate
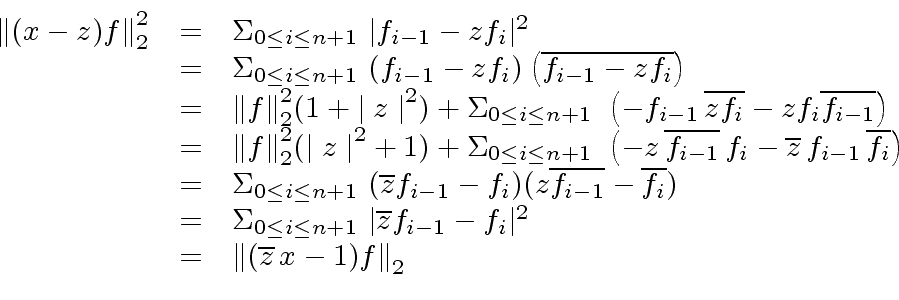 |
(75) |
![]()
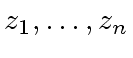 be the complex roots of the polynomial
be the complex roots of the polynomial
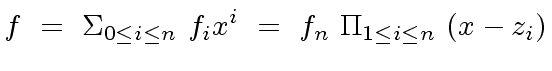 |
(76) |
We define the measure of the polynomial ![]() by
by
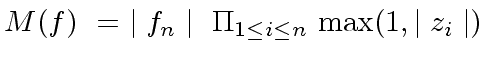 |
(77) |
![$ f,g \in {\mbox{${\mathbb{C}}$}}[x]$](img280.png) the following statements are easy to prove:
the following statements are easy to prove:
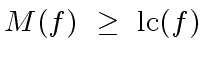 .
.
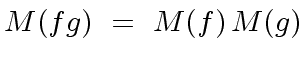 .
.
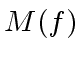 and
and
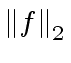 .
.
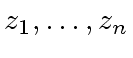 of
of 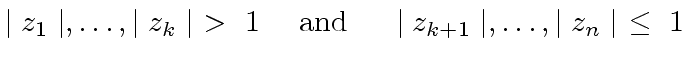 |
(79) |
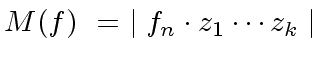 |
(80) |
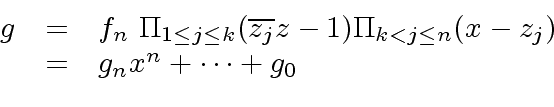 |
(81) |
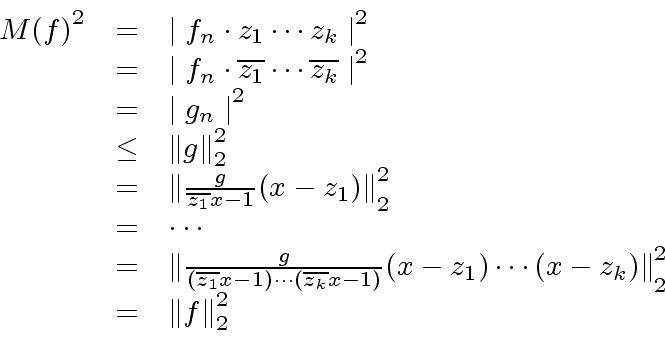 |
(82) |
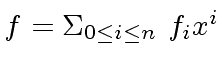 it is convenient to use the
it is convenient to use the 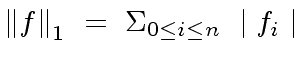 |
(83) |
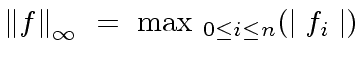 |
(84) |
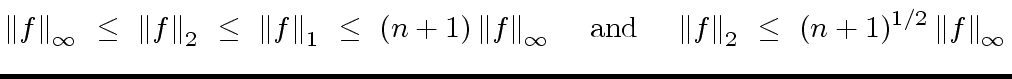 |
(85) |
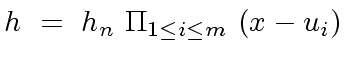 |
(87) |
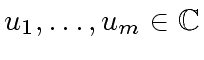 are the roots of
are the roots of 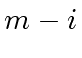 factors,
each of these factors being a root of
factors,
each of these factors being a root of 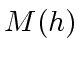 .
.
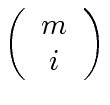 of these factors. Indeed, in order to build one of these factors, one needs to choose
of these factors. Indeed, in order to build one of these factors, one needs to choose
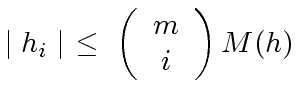 |
(88) |
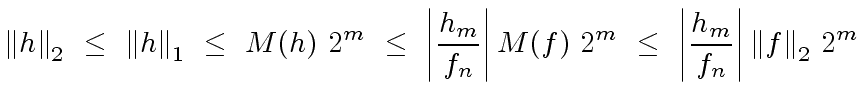 |
(91) |
![$ f,g,h \in {\mbox{${\mathbb{Z}}$}}[x]$](img308.png) be univariate polynomials with degrees
be univariate polynomials with degrees 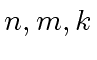 respectively.
If the product
respectively.
If the product ![$ {\mbox{${\mathbb{Z}}$}}[x]$](img46.png) then we have
then we have
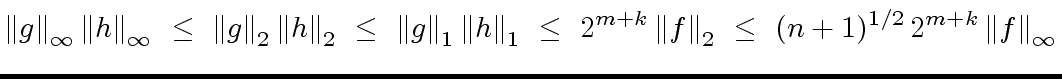 |
(92) |
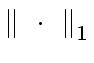 ,
,
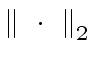 and
and
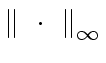 given in Remark 11.
So the only inequality to prove is
given in Remark 11.
So the only inequality to prove is
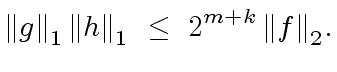 |
(93) |
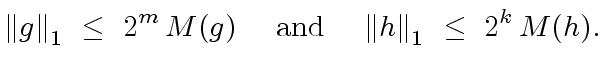 |
(94) |
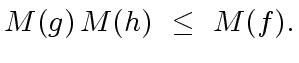 |
(95) |
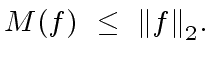 |
(96) |
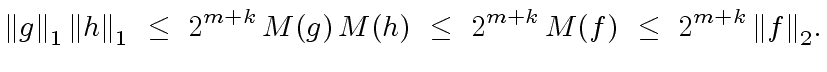 |
(97) |
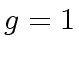 and keeping
and keeping 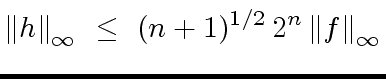 |
(98) |
Marc Moreno Maza