Next: Bibliography Up: Modular Computation Previous: Modular computation of the determinant
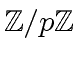 , for any machine-word size prime number
, for any machine-word size prime number
Consider two square matrices
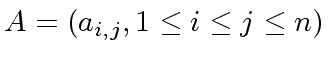 and
and
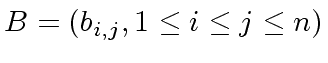 of order
of order ![]() with coefficients in
with coefficients in
![]() .
Let
.
Let
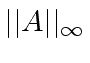 and
and
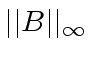 be the maximum absolute value
of a coefficient in
be the maximum absolute value
of a coefficient in ![]() and
and ![]() , respectively.
Let
, respectively.
Let
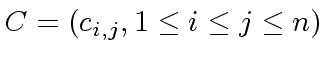 be the matrix product
be the matrix product
![]() and let
and let 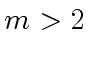 be any odd integer (prime or not).
For all
be any odd integer (prime or not).
For all
 , we have
, we have
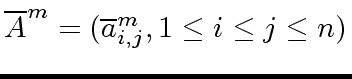 and
and
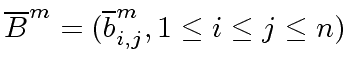 be the images of
be the images of 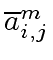 of
of
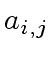 modulo
modulo 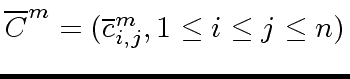 be the matrix product
be the matrix product
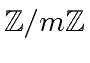 .
Hence, we have
.
Hence, we have
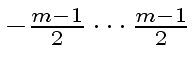 for representing the elements of
for representing the elements of
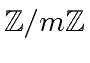 and if we have
and if we have
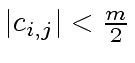 , then Equation (141)
simply becomes
, then Equation (141)
simply becomes
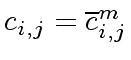 .
.
Observe that for all
 , we have
, we have
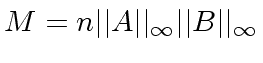 .
We are ready to state a modular algorithm.
.
We are ready to state a modular algorithm.
Note that the first for loop computes the matrcies
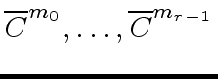 by the classical method.
However, one can use instead any other algorithm (like Strassen's)
computing these matrices.
Let us give an upper bound for the number of machine-word operations
required by Algorithm 6.
It suffices to estimate each of the two for loops.
The first one runs in
by the classical method.
However, one can use instead any other algorithm (like Strassen's)
computing these matrices.
Let us give an upper bound for the number of machine-word operations
required by Algorithm 6.
It suffices to estimate each of the two for loops.
The first one runs in 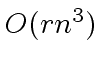 and the second one in
and the second one in
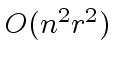 .
This is a better estimate than the one which can be given
for the naive (non-modular approach):
.
This is a better estimate than the one which can be given
for the naive (non-modular approach):
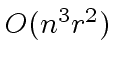 .
.
Marc Moreno Maza