Next: Modular computation of the matrix Up: Modular Computation Previous: Modular Arithmetic
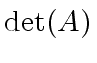 , the determinant of
, the determinant of 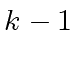 pivoting stages the current matrxi
pivoting stages the current matrxi 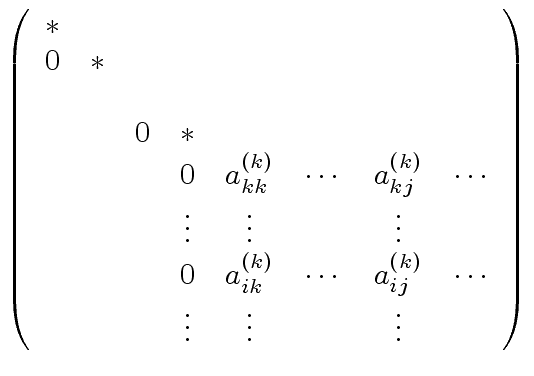 |
(110) |
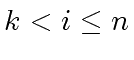 and
and
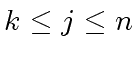 change according to the formula
change according to the formula
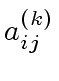 .
.
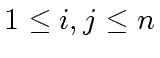 we have
we have
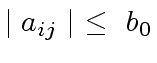 .
.
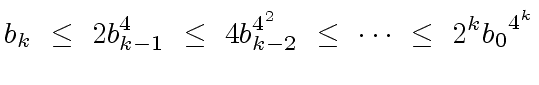 |
(112) |
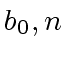 can be established
but the proof is far from trivial and the formula still not very encouraging.)
can be established
but the proof is far from trivial and the formula still not very encouraging.)
In what follows, we present an approach whose goal is to control
the growth of the intermediate computations when calculating the determinant of ![]() .
Let
.
Let ![]() be this determinant.
Let us choose a prime number
be this determinant.
Let us choose a prime number
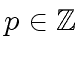 such that
such that
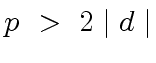 |
(113) |
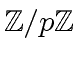 and let us choose for representing
and let us choose for representing
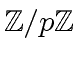 the integers in the symmetric range
the integers in the symmetric range
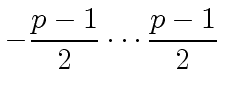 |
(114) |
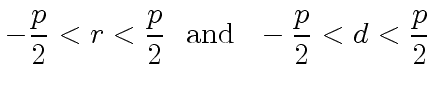 |
(115) |
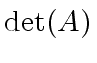 is a polynomial in the coefficients of
is a polynomial in the coefficients of 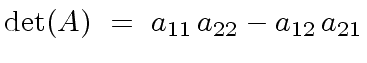 |
(117) |
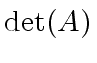 (for
(for 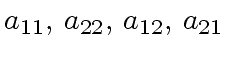 .
Observe also the map
.
Observe also the map
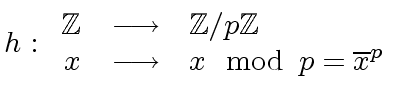 |
(118) |
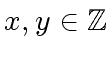 we have
we have
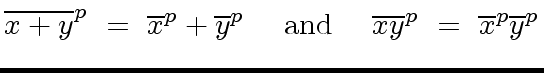 |
(119) |
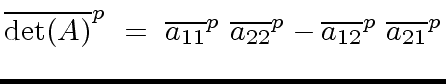 |
(120) |
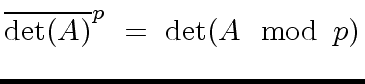 |
(121) |
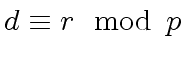 |
(122) |
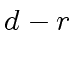 .
This with Relation (116) leads to
.
This with Relation (116) leads to
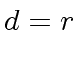 |
(123) |
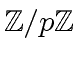 .
Therefore the computation of the determinant of
.
Therefore the computation of the determinant of
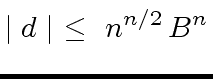 |
(124) |
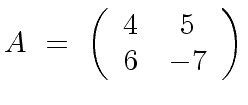 |
(125) |
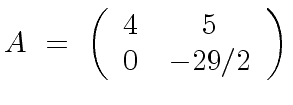 |
(126) |
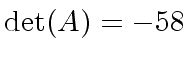 .
The Hadamard's inequality gives
.
The Hadamard's inequality gives
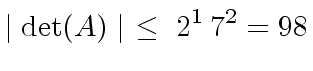 |
(127) |
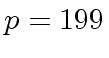 is prime and satisfies
is prime and satisfies
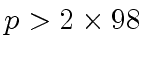 .
Gaussian elimination
.
Gaussian elimination
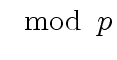 leads to
leads to
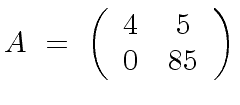 |
(128) |
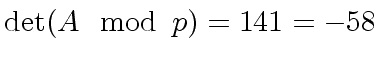 in
in
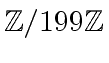 .
.
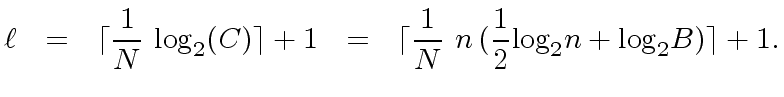 |
(129) |
 can be coded by an array
with at most
can be coded by an array
with at most
 words.
words.
 costs at most
costs at most
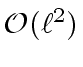 word operations.
word operations.
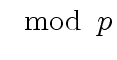 will require
will require
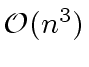 operations in
operations in
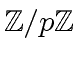 .
.
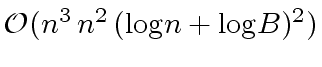 word operations.
word operations.
This is not in fact a big progress w.r.t. Gaussian elimination over
![]() .
But this can be improved using a small primes modular computation
as follows.
.
But this can be improved using a small primes modular computation
as follows.
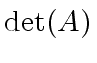 is a polynomial expression in the coefficients of
is a polynomial expression in the coefficients of 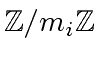 for
for
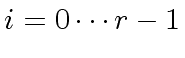 we have
we have
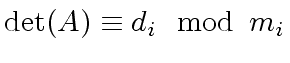 |
(130) |
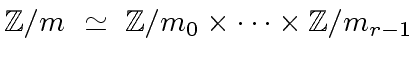 |
(131) |
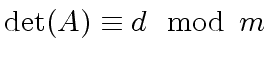 |
(132) |
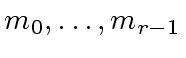 .
Now observe that
.
Now observe that
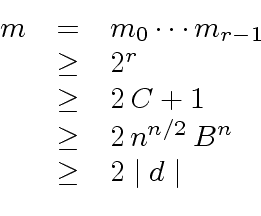 |
(133) |
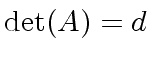 .
.
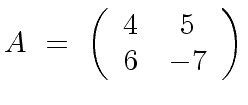 |
(134) |
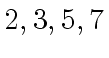 so that
so that 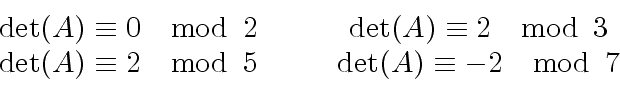 |
(135) |
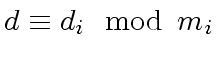 for
for
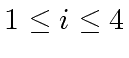 are in
are in
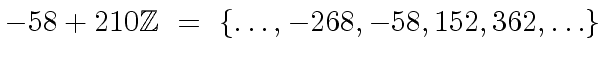 |
(136) |
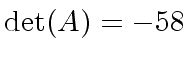 again.
again.
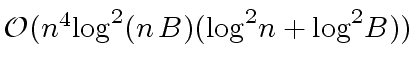 word operations.
word operations.
Marc Moreno Maza