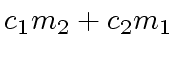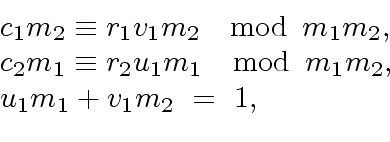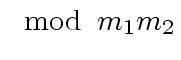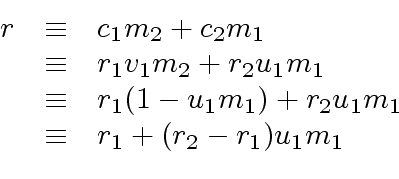We start with the elementary case of the
Chinese Remaindering Theorem
(Theorem 1).
Then we give a much more abstract version
(Theorem 2).
Then we state the Chinese Remaindering Theorem
and
the
Chinese Remaindering Algorithm
in the context of Euclidean domains.
Proof.
First observe that Relation (
46) implies
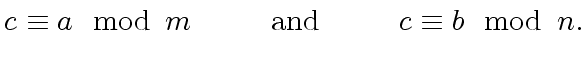 |
(48) |
Now assume that
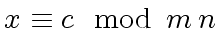
holds.
This implies
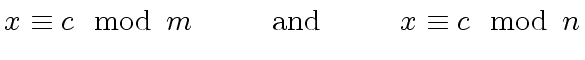 |
(49) |
Thus Relations (
48) and (
49) lead to
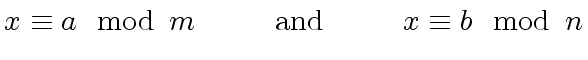 |
(50) |
Conversly
-
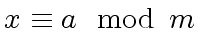 implies
implies
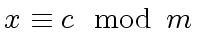 that is
that is 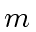 divides
divides 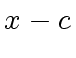 and
and
-
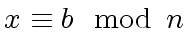 implies
implies
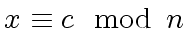 that is
that is 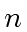 divides
divides 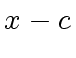 .
.
Since
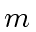
and
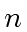
are relatively prime it follows that
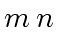
divides
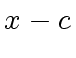
.
(Gauss Lemma).

Proof.
The first statement is obvious.
Let us prove the second one.
Let
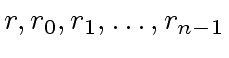
be in
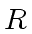
.
We look for the pre-image of
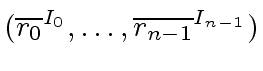
.
Hence we look for
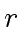
such that
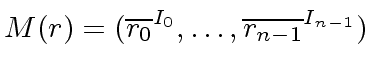 |
(53) |
that is
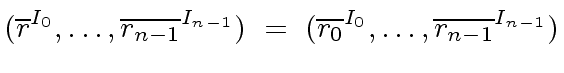 |
(54) |
or
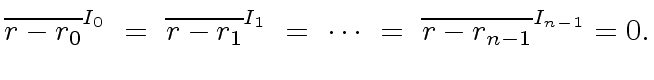 |
(55) |
At this point of the proof we need the following lemma.

Proof.
The equation
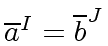
means that the residue classe of
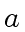
in
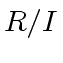
is equal
to the residue classe of
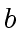
in
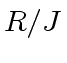
.
More formally we have
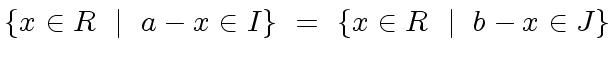 |
(57) |
or equivalently
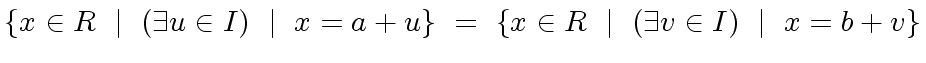 |
(58) |
Since these sets are non empty this implies
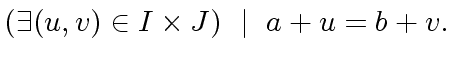 |
(59) |
Since
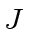
is an ideal we have
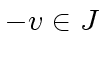
and thus
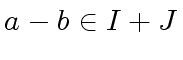 |
(60) |
The lemma is proved.

CONTINUING THEOREM'S
Proof.
With the previous lemma
Relation (
55),
for all
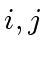
such that
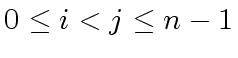
holds, leads to
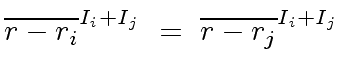 |
(61) |
or equivalently
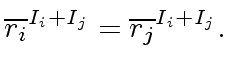 |
(62) |
Relation (
62) is a necessary condition
for the existence of a pre-image of
via the homomorphism
.
Therefore we proved the second statement of the theorem.
Let us prove the third one.
Let us ssume first that 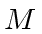 is surjective.
Let
is surjective.
Let 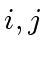 be such that
be such that
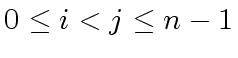 .
There exists
.
There exists 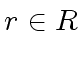 such that
such that
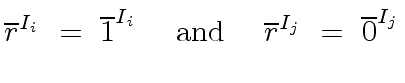 |
(63) |
Hence
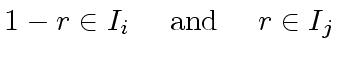 |
(64) |
which implies
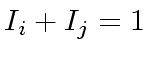
.
Conversly, let us assume that the ideals
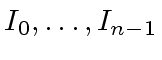
are pairwise coprime.
Let
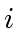
be in the range
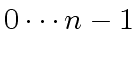
and consider
the product
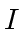
of all ideals
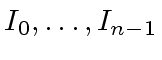
except
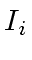
.
It is a classical result that
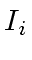
and
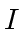
are coprime.
Let
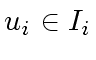
and
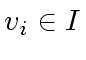
such that
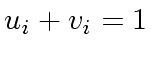
.
Observe that for all
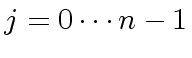
we have
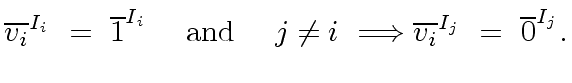 |
(65) |
Now consider
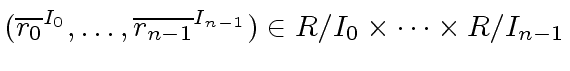
.
Then
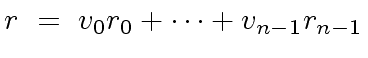 |
(66) |
satisfies
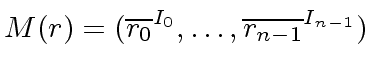 |
(67) |
This concludes the proof of the theorem.

Proof.
The following ring isomorphism follows from Theorem
2
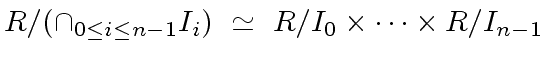 |
(70) |
It is a well known fact that if the ideals
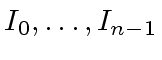
are pairwise coprime
(
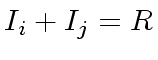
for every
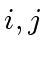
with
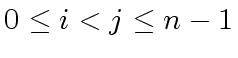
)
then their product is equal to their intersection [
van91].
Therefore, we have the ring isomorphism of the statement.
The group isomorphism follows from the previous ring isomorphism
and the fact that the element
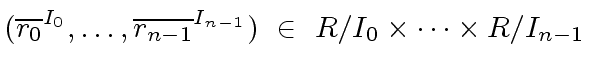 |
(71) |
is a unit iff every
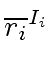
is a unit of
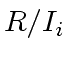
.

From now on 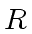 denotes an Euclidean domain.
denotes an Euclidean domain.
Proof.
Assume that the algorithm terminates without error,
that is the case if every
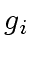
is
the gcd of
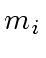
and
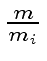
(which are assumed to be coprime).
Then, for
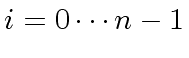
we have
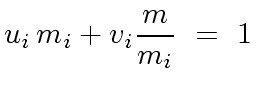 |
(74) |
Hence
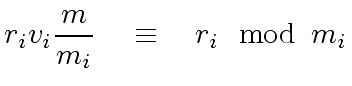 |
(75) |
and for
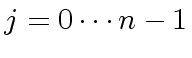
with
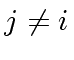
we have
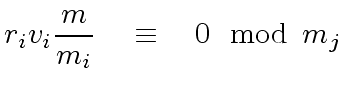 |
(76) |
The specification of Algorithm
4 follow
easily from Relation (
75) and (
76).

Proof.
Except for the complexity result (that can be found
in [
GG99] as Theorem 5.7) and the uniqueness, this theorem follows
from Algorithm
4.
The uniqueness follows from the constraint
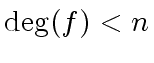
.
Indeed, assume that there are two polynomials
and
solutions
of (
80).
Then we have
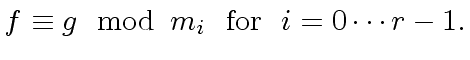 |
(81) |
and thus
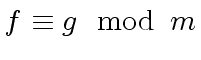 |
(82) |
Hence
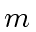
divides
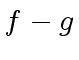
although
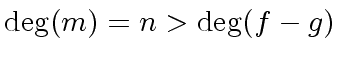
holds.
Therefore
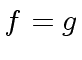
.

Proof.
Except for the complexity result (that can be found
in [
GG99] as Theorem 5.8) and the uniqueness,
this theorem follows
from Algorithm
4.
The proof of the uniqueness is quite easy to establish.

We reproduce below the ALDOR code for the Chinese Remaindering Algorithm.
More precisely, the operation interpolate satisfies exactly the
specification of Algorithm 4.
After the definition of the ChineseRemaindering domain
we prove that its operation combine satisifies the
specification of Algorithm 4
for the case of two moduli 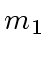 and
and 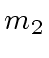 .
The reader is left with the proof of the operation interpolate
which implements the general case (with
.
The reader is left with the proof of the operation interpolate
which implements the general case (with  moduli).
moduli).
ChineseRemaindering(E: EuclideanDomain): with {
combine: (E, E) -> (E, E) -> E;
interpolate: (List E, List E) -> E;
} == add {
combine(m1: E, m2: E): (E, E) -> E == {
local u1: E;
assert(m1 = unitCanonical m1);
assert(m2 = unitCanonical m2);
fn(r1: E, r2: E): E == {
r1__new := r1 rem m1;
r := (r2 - r1__new) rem m2 ;
r := (r * u1) rem m2 ;
r := r1__new + r * m1;
}
(u1, u2, g) := extendedEuclidean(m1, m2);
fn
}
interpolate(lm: List E, lr: List E): E == {
m := first lm;
r := first lr rem m;
for mi in rest lm for ri in rest lr repeat {
r := combine(m, mi)(r, ri);
m := m * mi;
}
return r;
}
}
Marc Moreno Maza
2008-01-07
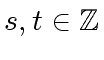 be such that
be such that
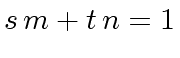 .
For every
.
For every
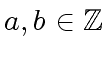 there exists
there exists
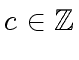 such that
such that
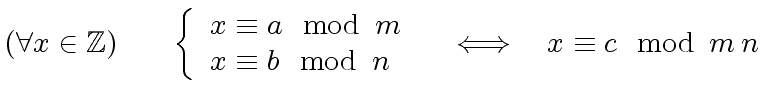
 the system
of equations
the system
of equations
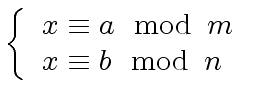
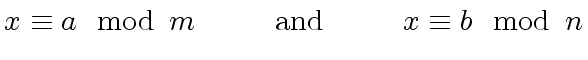
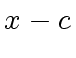 and
and
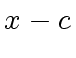 .
.
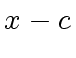 .
(Gauss Lemma).
.
(Gauss Lemma).
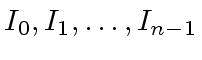 be ideals of
be ideals of 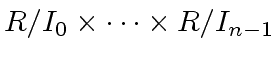 (additions and multiplications are computed componentwise)
together with the homomorphism
(additions and multiplications are computed componentwise)
together with the homomorphism
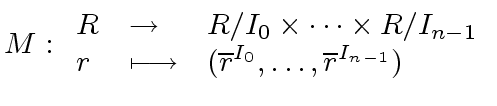
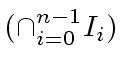 .
.
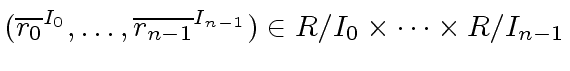 has a pre-image
has a pre-image 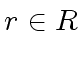 then we have
then we have
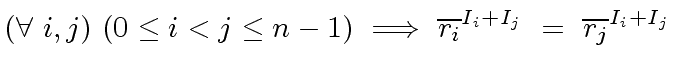
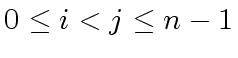 we have
we have
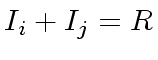 .
.
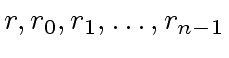 be in
be in 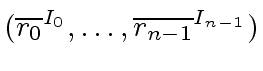 .
Hence we look for
.
Hence we look for 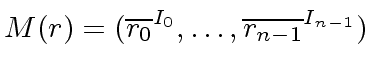
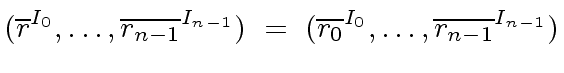
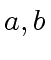 be two elements of the ring
be two elements of the ring 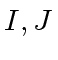 be two ideals of
be two ideals of 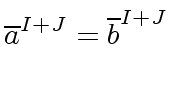
 is equal
to the residue classe of
is equal
to the residue classe of 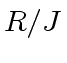 .
More formally we have
.
More formally we have
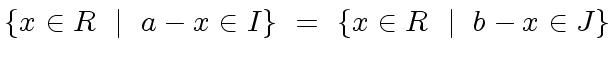
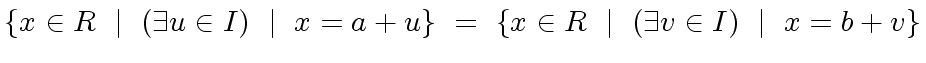
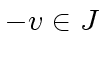 and thus
and thus
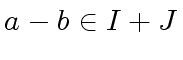
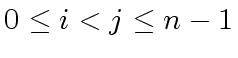 holds, leads to
holds, leads to
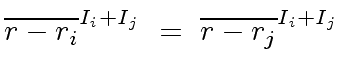
![]() is surjective.
Let
is surjective.
Let ![]() be such that
be such that
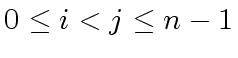 .
There exists
.
There exists 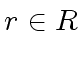 such that
such that
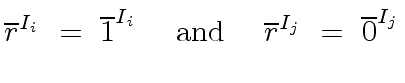
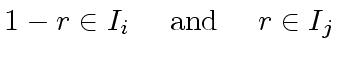
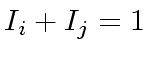 .
Conversly, let us assume that the ideals
.
Conversly, let us assume that the ideals
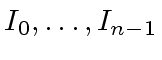 are pairwise coprime.
Let
are pairwise coprime.
Let 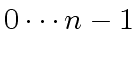 and consider
the product
and consider
the product 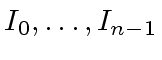 except
except 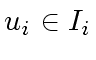 and
and 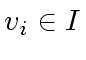 such that
such that
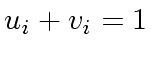 .
Observe that for all
.
Observe that for all
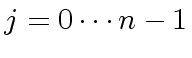 we have
we have
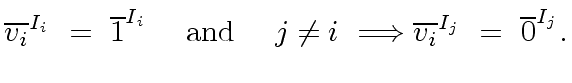
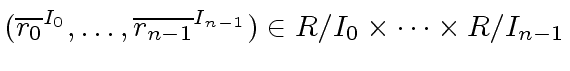 .
Then
.
Then
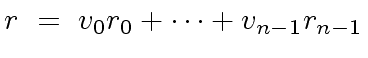
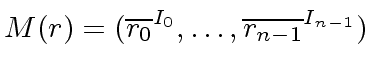
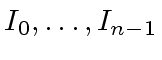 be ideals of
be ideals of 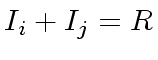 for every
for every 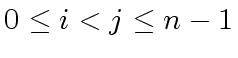 .
Let
.
Let 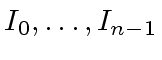 .
Then we have the ring isomorphism
.
Then we have the ring isomorphism
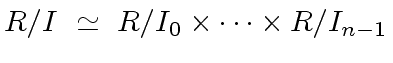
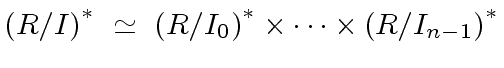
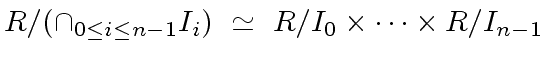
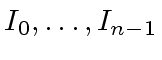 are pairwise coprime
(
are pairwise coprime
(
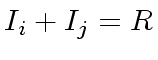 for every
for every 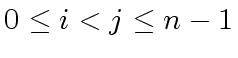 )
then their product is equal to their intersection [van91].
Therefore, we have the ring isomorphism of the statement.
The group isomorphism follows from the previous ring isomorphism
and the fact that the element
)
then their product is equal to their intersection [van91].
Therefore, we have the ring isomorphism of the statement.
The group isomorphism follows from the previous ring isomorphism
and the fact that the element
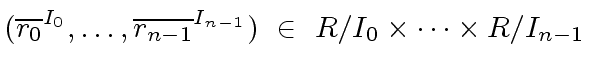
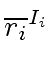 is a unit of
is a unit of 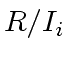 .
.
![]() denotes an Euclidean domain.
denotes an Euclidean domain.
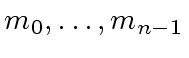 be
be 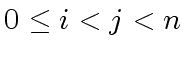 we have
we have
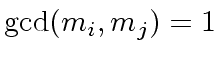 .)
Let
.)
Let
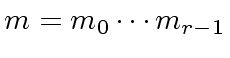 .
Then, we have the ring isomorphism
.
Then, we have the ring isomorphism
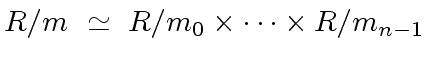
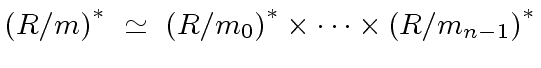
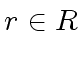 such that
such that 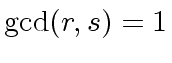 .
.
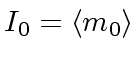 ,
...
,
...
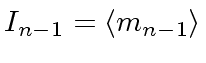 .
.
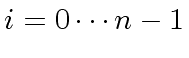 we have
we have
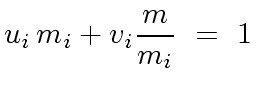
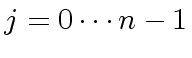 with
with 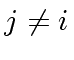 we have
we have
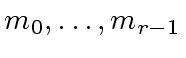 .
This follows from the fact the
.
This follows from the fact the 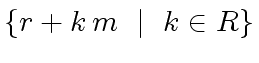
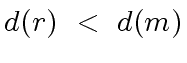
![$ R = {\bf k}[x]$](img19.png) for a field
for a field 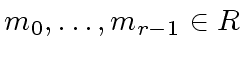 be polynomials
pairwise coprime (
be polynomials
pairwise coprime (
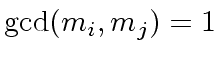 for
for
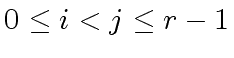 ).
Let
).
Let 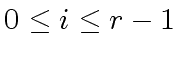 let
let
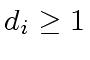 be the degree of
be the degree of 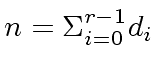 be the degree of
be the degree of 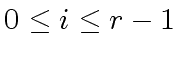 let
let
![$ f_i \in {\bf k}[x]$](img336.png) be a polynomial with degree
be a polynomial with degree
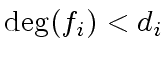 .
Then there is a unique polynomial
.
Then there is a unique polynomial
![$ f \in {\bf k}[x]$](img202.png) such that
such that
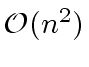 operations in
operations in 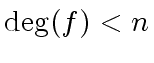 .
Indeed, assume that there are two polynomials
.
Indeed, assume that there are two polynomials 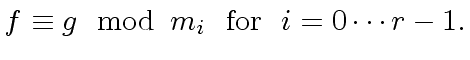
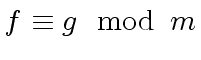
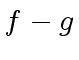 although
although
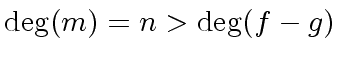 holds.
Therefore
holds.
Therefore 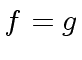 .
.
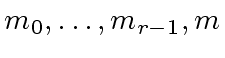 be in
be in
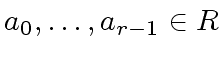 be such that
be such that
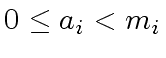 for
for
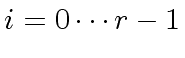 .
Then there is a unique
.
Then there is a unique 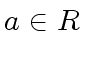 such that
such that
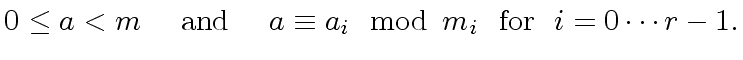
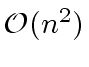 word operations.
word operations.![]() and
and ![]() .
The reader is left with the proof of the operation interpolate
which implements the general case (with
.
The reader is left with the proof of the operation interpolate
which implements the general case (with  moduli).
moduli).
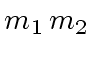 .
.
![]() and
and ![]() requires the following computations
requires the following computations
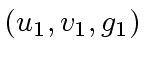 := extendedEuclidean(
:= extendedEuclidean(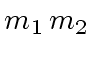 )
)
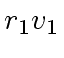 rem
rem 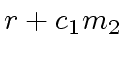
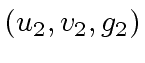 := extendedEuclidean(
:= extendedEuclidean(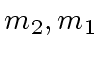 )
)
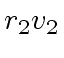 rem
rem 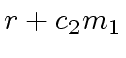
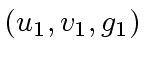 := extendedEuclidean(
:= extendedEuclidean(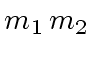 )
)
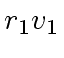 rem
rem 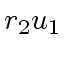 rem
rem