Next: Fast Extended Euclidean Algorithm Up: Division with remainder using Newton Previous: Modular inverses using Newton iteration
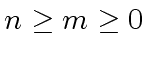 and
and 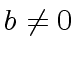 monic.
Algorithm 3
computes the quotient and the remainder of
monic.
Algorithm 3
computes the quotient and the remainder of 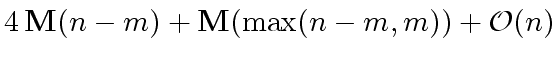 operations in
operations in
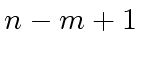 ,
plus operations in
,
plus operations in
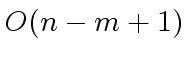 operations in
operations in 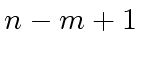 to compute
to compute 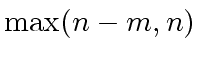 ,
and one subtraction in degree
,
and one subtraction in degree
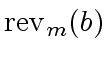 modulo some powers
modulo some powers
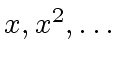 of
of
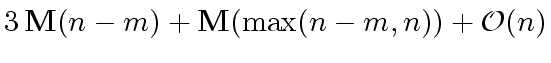 if the middle product technique
described in Remark 6
applies.
Moreover, if
if the middle product technique
described in Remark 6
applies.
Moreover, if
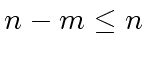 holds, the
holds, the
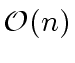 can be repalced by
can be repalced by
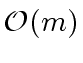 .
.
Marc Moreno Maza