Next: What are our requirements for Up: How to encode the elements Previous: Univariate polynomials.
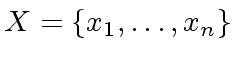 be a finite set of variables.
The multivariate polynomial ring
be a finite set of variables.
The multivariate polynomial ring ![$ R[X]$](img201.png) can be implemented in different ways.
can be implemented in different ways.
RECURSIVELY.
![$ R[X]$](img201.png) as a univariate
polynomial ring with a multivariate polynomial
ring as coefficient ring, say for instance
as a univariate
polynomial ring with a multivariate polynomial
ring as coefficient ring, say for instance
![$ R[x_1, \ldots, x_{n-1}][x_n]$](img202.png) .
.
AS LINEAR COMBINATIONS OF MONOMIALS.
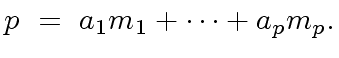 |
(36) |
![$ [a_i, m_i]$](img205.png) .
.
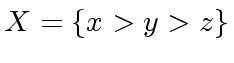 we have
we have
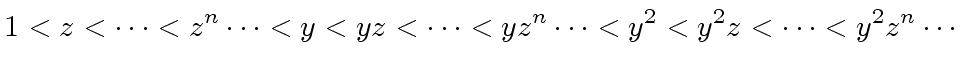 |
(37) |
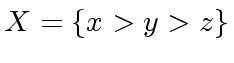 we have
we have
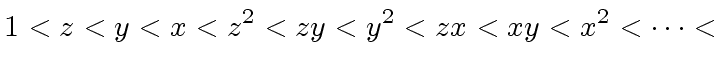 |
(38) |
Marc Moreno Maza