Next: Gcd Algorithms in where is Up: Advanced Computer Algebra: The resultant Previous: A modular Gcd Algorithm in
![$ E[x]$](img4.png) with
with
First we assume that we have access to the stream of unassociated primes
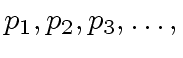 such that
such that
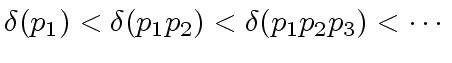 .
Indeed the recovery of an element
.
Indeed the recovery of an element ![]() in
in ![]() from
from
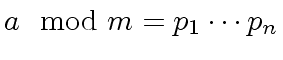 requires sufficiently large
requires sufficiently large ![]() .
.
Secondly, we assume the avialability of a mapping
![]() from
from
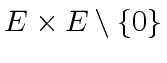 to
to ![]() , called a symmetric canonical simplifier,
such that we have the following properties.
, called a symmetric canonical simplifier,
such that we have the following properties.
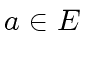 must satisfy
must satisfy
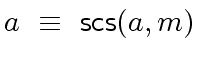 for any
for any
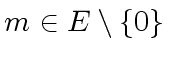 . More formally:
. More formally:
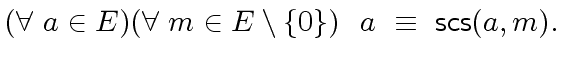 |
(116) |
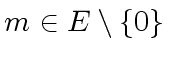 ,
any two elements
,
any two elements 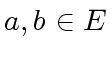 equivalent modulo
equivalent modulo 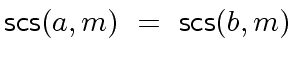 . More formally:
. More formally:
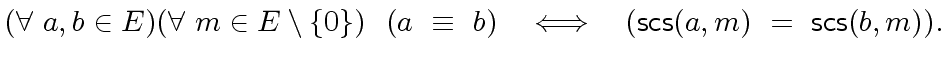 |
(117) |
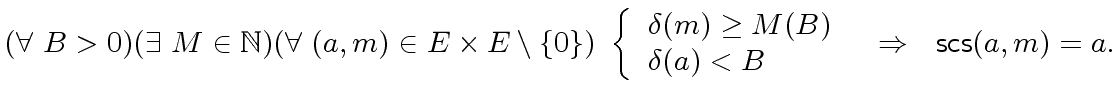 |
(118) |
See [KM99] for more details.
Marc Moreno Maza