We consider the following 4 square matrices of order 2 with coefficients in
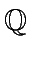 :
:
Then we consider the following polynomials of degree 1 in 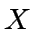 and with
square matrices of order 2 for coefficients:
and with
square matrices of order 2 for coefficients:
- How many additions and multiplications in
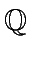 are needed
in order to compute the product
are needed
in order to compute the product 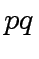 in a naive way.
in a naive way.
- Check that Karatsuba's trick applies here (despite of the
fact that matrix multiplication is not commutative).
- Explain briefly why we can compute
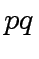 using only 21 multiplications in
using only 21 multiplications in
 .
How many additions in
.
How many additions in
 are needed in this case?
are needed in this case?
- Explain briefly in which circumstances using the
multiplication scheme of the previous question makes sense.
![\fbox{
\begin{minipage}{15 cm}
\begin{enumerate}
\item[1.] We have:
\begin{equat...
... applies to polynomials with matrix coefficients.
\end{enumerate}\end{minipage}}](img55.png)
![\fbox{
\begin{minipage}{13 cm}
\begin{enumerate}
\item[3.] Applying Karatsuba's ...
...tions.
The GCD computations dominane both costs.
\end{enumerate}\end{minipage}}](img56.png)
Marc Moreno Maza
2008-01-31
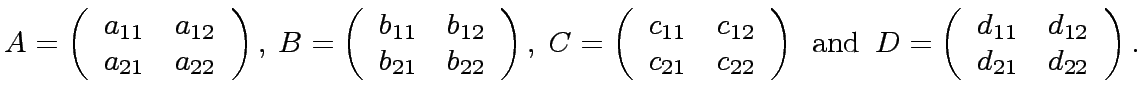
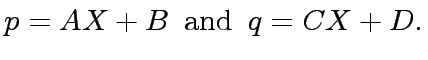
![\fbox{
\begin{minipage}{15 cm}
\begin{enumerate}
\item[1.] We have:
\begin{equat...
... applies to polynomials with matrix coefficients.
\end{enumerate}\end{minipage}}](img55.png)
![\fbox{
\begin{minipage}{13 cm}
\begin{enumerate}
\item[3.] Applying Karatsuba's ...
...tions.
The GCD computations dominane both costs.
\end{enumerate}\end{minipage}}](img56.png)