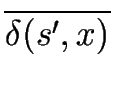

Next: About this document ...
Up: The design of an efficient
Previous: The design of an efficient
EQUIVALENCE OF WORDS MODULO A LANGUAGE. Let
L 
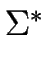 be a language over the alphabet
be a language over the alphabet 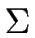 .
Let
u, v
.
Let
u, v 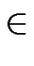
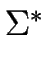 be two words (that may belong or not
to the language L).
We say that the language L SEPARATES u et v if
be two words (that may belong or not
to the language L).
We say that the language L SEPARATES u et v if
We say that u et v are equivalent modulo L and we write
u 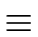 v mod L if for every
w
v mod L if for every
w 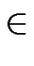
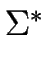 the language L
does not separate the words u w and v w.
In other words we have
the language L
does not separate the words u w and v w.
In other words we have
u 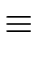 v mod L v mod L 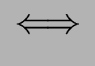 ( ( w w 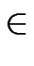 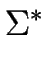 ) ) 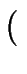 u w u w 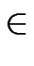 L L  v w v w 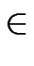 L L |
(15) |
The relation
u  v mod L is an equivalence relation
(since it is reflexive, symmetric and transitive) and thus
defines equivalence classes called the equivalence
classes (or residue classes) associated with L.
v mod L is an equivalence relation
(since it is reflexive, symmetric and transitive) and thus
defines equivalence classes called the equivalence
classes (or residue classes) associated with L.
EQUIVALENCE OF WORDS MODULO AN AUTOMATON. Let
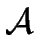 = (
= (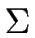 , S, i, F,
, S, i, F,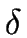 ) be a DFA.
Let
u, v
) be a DFA.
Let
u, v 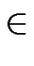
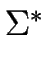 be two words
We say that u et v are equivalent modulo
be two words
We say that u et v are equivalent modulo 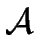 and we write
u
and we write
u  v mod
v mod 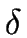 if after reading u
the DFA is in the same state than after reading v.
Let us denote by
if after reading u
the DFA is in the same state than after reading v.
Let us denote by
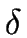 (i, u) and
(i, u) and
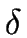 (i, v)
the state of the automaton
(i, v)
the state of the automaton 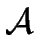 after reading u and v respectively.
Then we have
after reading u and v respectively.
Then we have
u  v mod v mod 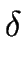  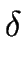 (i, u) = (i, u) = 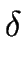 (i, v). (i, v). |
(16) |
Again the relation
u  v mod
v mod 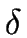 is an equivalence relation and thus defines
residue classes associated with the automaton
is an equivalence relation and thus defines
residue classes associated with the automaton 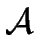 .
.
Example 6
The DFA over
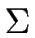
= {
a,
b}
on Figure
20 has three residue classes:
- that of the words with no a,
- that of the words with no b after an a,
- that of the words with a factor ab.
Figure 20:
A DFA whith three classes of equivalence.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.5]{nonMinimalAutomaton.eps}
\end{figure}](img94.png) |
Proposition 8
Let
L 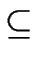
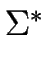
be a language over
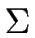
recognized by the DFA
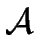
= (
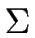
,
S,
i,
F,
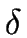
).
For every words
u and
v we have
Remark 4
Proposition 8
expresses the fact that every residue class modulo the automaton 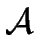 is entirely contained in a residue class modulo its associated language L.
Therefore the number of classes modulo L is upper bounded by
the number of classes modulo
is entirely contained in a residue class modulo its associated language L.
Therefore the number of classes modulo L is upper bounded by
the number of classes modulo 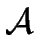 and thus by the
number of states of
and thus by the
number of states of 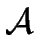 .
It follows from the following theorem that
having a finite number of residue classes
is a necessary and sufficient condition
for a language to be recognized by FA.
.
It follows from the following theorem that
having a finite number of residue classes
is a necessary and sufficient condition
for a language to be recognized by FA.
Theorem 4
Let
L 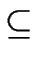
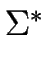
be a language over the alphabet
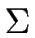
.
Let
n be a positive integer.
If there exist exactly
n residue classes modulo
L
then there exists a DFA with
n states that recognizes
L.
MINIMAL AUTOMATON. Let
L 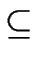
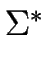 be a language over the alphabet
be a language over the alphabet 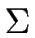
- recognized by FA and
- with n residue classes.
It follows from Proposition 8
and Theorem 4 that
- every DFA recognizing L has at least n states,
- there exists a DFA with n states recognizing L.
Therefore we can call minimal automaton every DFA with n states
and recognizing L.
Remark 5
The number of residue classes of a language is rarely known
(until one gets a minimal DFA accepting this language).
So one needs a way to characterize minimal automata.
Then one needs an algorithm to compute from a given DFA (minimal or not)
recognizing L a minimal automaton recognizing L too.
Such an algorithm will group states
that do essentially the same job.
This leads to the following notions.
EQUIVALENCE OF STATES IN A DFA. Let
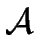 = (
= (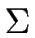 , S, i, F,
, S, i, F,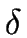 ) be a DFA.
We say that two states p, q
) be a DFA.
We say that two states p, q 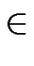 S are equivalent
and we write
p
S are equivalent
and we write
p  q if for every word
w
q if for every word
w 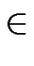
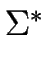 we have
we have
(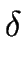 (p, w) (p, w) 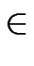 F) F) ( (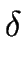 (q, w) (q, w) 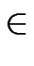 F). F). |
(18) |
Let k be a non-negative integer.
We say that two states p, q 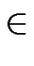 S are equivalent at order k
and we write
p
S are equivalent at order k
and we write
p 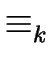 q if for every word
w
q if for every word
w 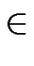
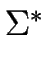 with length
| w |
with length
| w |
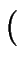 | w | | w | 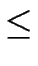 k k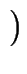  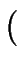 ( (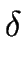 (p, w) (p, w) 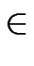 F) F)  ( (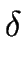 (q, w) (q, w) 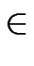 F) F)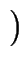 |
(19) |
CHARACTERIZATION OF A MINIMAL AUTOMATON. Among other properties,
Theorem 5
states that for a minimal
automaton, each residue class of states contains only
one state.
CONSTRUCTION OF THE EQUIVALENCE CLASSES FOR STATES. Proposition 9
suggests an algorithm for constructing the equivalence classes
of states.
Proposition 9
Let
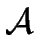
= (
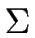
,
S,
i,
F,
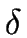
) be a DFA
and
k be a non-negative integer.
If the relations
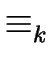
and
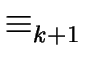
have the same residue classes
then
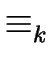
and
have the same residue classes too.
The method is follows.
- Compute
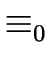 which consists
of two classes:
which consists
of two classes:
- the set of the final states,
- the set of the non final states.
- Compute
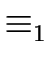 and set k to 0
and set k to 0
- Whhile
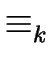 and
and
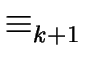 are different
are different
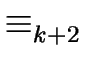 and set k to k + 1.
and set k to k + 1.
In practice one construct a table that gives
the transition from each state after
reading any word of length 0, any word of length 1, any word of length 2, etc...
In these tables we underline final states in order to detect classes
more easily.
Quite often computations can be simpler.
For instance, in Example 7
computations can be stopped after computing the third column.
Explain why!
THE CONSTRUCTION OF A MINIMAL AUTOMATON
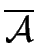 = (
= (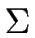 , S', i', F',
, S', i', F',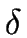
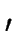 )
from a given DFA
)
from a given DFA
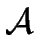 = (
= (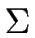 , S, i, F,
, S, i, F,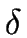 ) can be down as follows
(where the class of a state s
) can be down as follows
(where the class of a state s 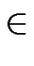 S is denoted by
S is denoted by
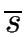 ).
).


Next: About this document ...
Up: The design of an efficient
Previous: The design of an efficient
Marc Moreno Maza
2004-12-02
![]()
![]() be a language over the alphabet
be a language over the alphabet ![]() .
Let
u, v
.
Let
u, v ![]()
![]() be two words (that may belong or not
to the language L).
We say that the language L SEPARATES u et v if
be two words (that may belong or not
to the language L).
We say that the language L SEPARATES u et v if
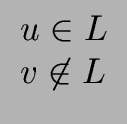 ou
ou 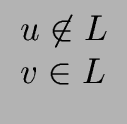
 (
( v w
v w ![]() = (
= (![]() , S, i, F,
, S, i, F,![]() ) be a DFA.
Let
u, v
) be a DFA.
Let
u, v ![]()
![]() be two words
We say that u et v are equivalent modulo
be two words
We say that u et v are equivalent modulo ![]() and we write
u
and we write
u ![]() v mod
v mod ![]() if after reading u
the DFA is in the same state than after reading v.
Let us denote by
if after reading u
the DFA is in the same state than after reading v.
Let us denote by
![]() (i, u) and
(i, u) and
![]() (i, v)
the state of the automaton
(i, v)
the state of the automaton ![]() after reading u and v respectively.
Then we have
after reading u and v respectively.
Then we have

 u
u ![]()
![]() be a language over the alphabet
be a language over the alphabet ![]()
![]() = (
= (![]() , S, i, F,
, S, i, F,![]() ) be a DFA.
We say that two states p, q
) be a DFA.
We say that two states p, q ![]() S are equivalent
and we write
p
S are equivalent
and we write
p ![]() q if for every word
w
q if for every word
w ![]()
![]() we have
we have
 (
(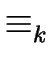 q if for every word
w
q if for every word
w 
 (
(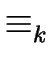 and
and
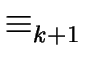 have the same residue classes
then
have the same residue classes
then
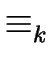 and
and 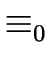 which consists
of two classes:
which consists
of two classes:
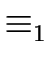 and set k to 0
and set k to 0
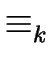 and
and
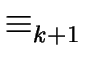 are different
are different
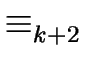 and set k to k + 1.
and set k to k + 1.
![]() = (
= (![]() , S', i', F',
, S', i', F',![]()
![]() )
from a given DFA
)
from a given DFA
![]() = (
= (![]() , S, i, F,
, S, i, F,![]() ) can be down as follows
(where the class of a state s
) can be down as follows
(where the class of a state s ![]() S is denoted by
S is denoted by
![]() ).
).
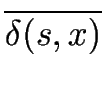 =
= 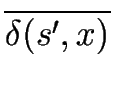 .
Hence we can define
.
Hence we can define