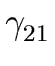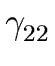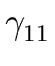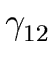

Next: Left factoring
Up: Context-free grammars
Previous: Elimination of ambiguity.
LEFT RECURSION.
Let G be a context-free grammar.
A production of G is said left recursive if it has
the form
A  A A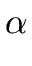 |
(20) |
where A is a nonterminal and  is a string of grammar symbols.
A nonterminal A of G is said left recursive
if there exists a string of grammar symbols
is a string of grammar symbols.
A nonterminal A of G is said left recursive
if there exists a string of grammar symbols
 such that we have
such that we have
A  A A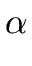 |
(21) |
Such derivation is also said left recursive.
The grammar G is left recursive if it has
at least one left recursive nonterminal.
Remark 4
Top-down parsing is one of the methods that
we will study for generating parse trees.
This method cannot handle left recursive grammars.
We present now an algorithm for transforming
a left recursive grammar G into a grammar G' which is not
left recursive and which generates the same language as G.
THE BASIC TRICK is to replace the production
where

 is assumed.
Observe that this trick eliminates left recursive productions.
Applying this trick is not enough to remove all derivations
of the form
A
is assumed.
Observe that this trick eliminates left recursive productions.
Applying this trick is not enough to remove all derivations
of the form
A  A
A .
However this trick is sufficient for many grammars.
.
However this trick is sufficient for many grammars.
THE CASE OF SEVERAL LEFT RECURSIVE A-PRODUCTIONS. Assume that the set of all A-productions has the form
A  A A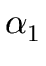 | A | A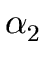 | ... A | ... A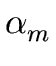 | | 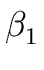 | | 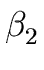 | ... | ... 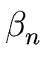 |
(25) |
where no 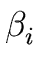 begins with an A and where
begins with an A and where
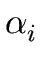
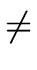
 holds for every
i = 1 ... m.
Then we repalce these A-productions by
holds for every
i = 1 ... m.
Then we repalce these A-productions by
| A |
 |
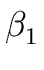 A' | A' | 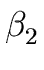 A' | ... A' | ... 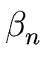 A' A' |
| A' |
 |
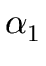 A' | A' | 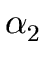 A' | ... A' | ... 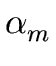 A' | A' | 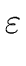 |
|
(26) |
Remark 5
Let us consider the following grammar.
The nonterminal S is left recursive since we have
S  Aa Aa  Sda Sda |
(28) |
However there is no left recursive S-productions.
We show now how to deal with these left recursive derivations.
REMOVING ALL LEFT RECURSIVE DERIVATIONS. Let us assume that non-terminals are numbered:
A1, A2,..., An.
The goal is to remove any possible circuit for all
1 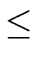 j < i
j < i 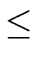 n
n
The idea is for
i = 1 ... n
- To make sure that every Ai-production does
not have a form
Ai
 Aj
Aj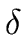 for some j < i.
for some j < i.
- To remove any left recursive Ai-production.
The method in more detail:
- remove all left recursive A1-productions
(by the above trick)
- remove A1 from the right-hand side of each
A2-production of the form
A2
 A1
A1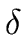 (by applying all A1-productions)
(by applying all A1-productions)
- remove all left recursive A2-productions
- remove Aj from the right-hand side of each
A3-production of the form
A3
 Aj
Aj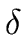 for j = 1, 2.
for j = 1, 2.
- remove all left recursive A3-productions
- ...
- remove Aj from the right-hand side of each
Ai-production of the form
Ai
 Aj
Aj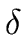 (for every j such that
1
(for every j such that
1 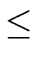 j < i
j < i 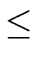 n)
n)
- remove all left recursive Ai-productions
- ...
Observations:
Example 11
Consider the following grammar.
Applying the previous algorithm for removing all possible left-recursive
derivations fail on this grammar, because of the
 -production.
-production.


Next: Left factoring
Up: Context-free grammars
Previous: Elimination of ambiguity.
Marc Moreno Maza
2004-12-02
 A
A A
A A
A A
A |
| ![]() j < i
j < i ![]() n
n
 Aj
Aj Ai
Ai Aj
Aj

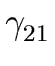 A2
A2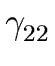 and
and
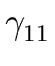 A1
A1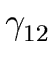 with
with