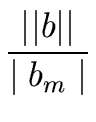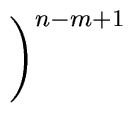Proposition 5
Let
a and
b two univariate polynomials in
R[
x] with respective degrees
n and
m such that
n 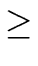 m
m 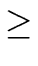
0 and the leading
coefficient of
b is a unit.
Then there exist unique polynomials
q and
r such that
a =
bq +
r and
deg
r <
m.
The polynomials
q and
r are called the
quotient and the
remainder of
a w.r.t. to
b.
Algorithm
5 compute them
in
(2
m + 1)(
n -
m + 1)
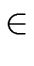
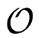
(
n m) operations in
R.
Proof.
We leave to the reader the proof of the uniqueness of the
quotient and the remainder of
a w.r.t. to
b.
So we focus now on the complexity result
Consider an iteration of the
for loop
where
deg
r =
m +
i holds at the begining of the loop.
Observe that
r and
qixib have the same leading coefficient.
Since
deg
b =
m, computing the reductum of
qixib requires
m operations.
Then subtracting the reductum of
qixib to that of
r requires again
m operations.
Hence each iteration of the
for loop requires at most 2
m + 1 operations in
R,
since we need also to count 1 for the computation of
qi.
The number of
for loops is
n -
m + 1.
Therefore Algorithm
5
requires
(2
m + 1)(
n -
m + 1).

![\fbox{
\begin{minipage}{12 cm}
\begin{description}
\item[{\bf Input:}] univariat...
...a}_{0}^{n-m} \ q_i x^i$\ \\
\> {\bf return} $(q,r)$\end{tabbing}\end{minipage}}](img126.png)