

Next: The Discrete Fourier Transform
Up: Fast Polynomial Multiplication based on
Previous: Fast Polynomial Multiplication based on
Let us recall that an element a 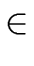 R is a zero divisor
if a
R is a zero divisor
if a 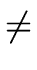 0 and there exists b
0 and there exists b 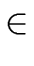 R such that
a b = 0 and b
R such that
a b = 0 and b 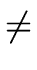 0.
0.
Let us recall also that because the ring R has a unit 1
then there is a map
which allows to talk of an integer as an element of R.
However a nonzero integer n may become 0R.
For instance every multiple of p becomes 0 in
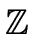 /p
/p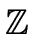 .
.
Observe also the ring R may contain nonzero elements that are neither
zero divisor, nor units. For instance in the ring of square
matrices of order 2 with integer coefficients the matrix
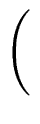
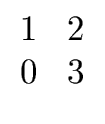
 is nonsingular but has no inverse (right or left).
But this is not a good example since we limit ourselves
to commutative rings. So consider instead the following example.
is nonsingular but has no inverse (right or left).
But this is not a good example since we limit ourselves
to commutative rings. So consider instead the following example.
Example 1
Let
R = 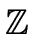 /6
/6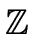 and let U = R[x] be
the ring of univariate polynomials over R.
The ring U has units (for instance the constant polynomial 5),
it has zero divisors (for instance the polynomial
2x + 4 since
3(2x + 4) = 0) and also
elements like x + 1 which is not a unit nor
a zero divisor.
and let U = R[x] be
the ring of univariate polynomials over R.
The ring U has units (for instance the constant polynomial 5),
it has zero divisors (for instance the polynomial
2x + 4 since
3(2x + 4) = 0) and also
elements like x + 1 which is not a unit nor
a zero divisor.
Why do we need to take such exotic examples?
Because among the rings you are familiar with, this is
the simplest example of ring having zero divisors, units
and nonzero elements that are not zero divisors or units.
Indeed our usual rings are
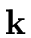 [x] where
[x] where 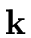 is a field and the residue class ring
is a field and the residue class ring
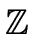 /m
/m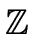 (with m > 1 not necessarily prime).
The ring
(with m > 1 not necessarily prime).
The ring
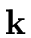 [x] has no zero divisors
whereas
[x] has no zero divisors
whereas
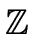 /m
/m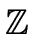 has zero divisors iff m is not prime.
But for every non prime m the ring
has zero divisors iff m is not prime.
But for every non prime m the ring
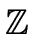 /m
/m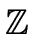 consists only of zero, units and zero divisors.
This follows from the proposition below.
This is why we were led to the
consists only of zero, units and zero divisors.
This follows from the proposition below.
This is why we were led to the
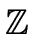 /6
/6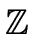 [x] example.
[x] example.
Proposition 1
Let
E be an Euclidean domain and
m an element of
E
with
m 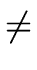
0 and
m 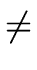
1.
Consider the residue class ring
R =
E/
 m
m
where
 m
m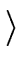
denotes the ideal generated by
m.
Then every element of
R is either zero, a zero divisor or a unit.
Proof.
Studying the elements of
R (for deciding if they
are null, zero divisors or units) can be done
by studying the
a mod
m for every
a 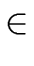 E
E.
So let
a be in
E.
If
a is a multiple of
m then
a 
0 mod
m.
Assume from now on that
a is not a a multiple of
m.
Consider
g the gcd of
a and
m together with the Bezout relation
Observe that
u mod
m cannot be zero
(otherwise
g mod
m would be zero
and
m would divide
g and thus
a).
If
g = 1 then
u a 
1 mod
m
and this shows
a mod
m is a unit of
R.
The same result holds if
g is a unit.
Assume from now on that
g is not a unit.
Since
g divides
a and
m let
a' and
m' be such that
| a = g a' and m = g m' |
(3) |
Observe that
m'mod
m is not zero
(otheriwse
m' would write
m' =
m''m
leading to the contradiction
g m'' = 1).
We have
m' a = m' g a' = m a'  0 mod m 0 mod m |
(4) |
This shows that
a mod
m is a zero divisor of
R.
Yes, this was that simple!

Remark 1
When R is an integral domain the last condition of Definition 1
becomes: for every prime divisor t of n the element
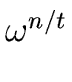
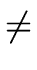 1.
Observe also that a n-th root of unity is necessarily a unit.
1.
Observe also that a n-th root of unity is necessarily a unit.
Example 2
Consider that R is the field
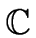 of complex numbers.
The number
of complex numbers.
The number
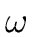 = e2
= e2 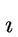
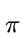 /8 is a
a primitive 8-th root of unity.
/8 is a
a primitive 8-th root of unity.
Example 3
In
R = 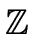 /8
/8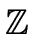 we have
32
we have
32 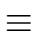 1.
However 3 is not a primitive 2-th of unity, since
n = 2 is not a unit in R.
1.
However 3 is not a primitive 2-th of unity, since
n = 2 is not a unit in R.
Example 4
In
R = 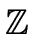 /17
/17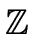 we have the following computation in AXIOM
we have the following computation in AXIOM
(1) -> R := PF(17)
(1) PrimeField 17
Type: Domain
(2) -> w: R := 3
(2) 3
Type: PrimeField 17
(3) -> [w^i for i in 0..16]
(3) [1,3,9,10,13,5,15,11,16,14,8,7,4,12,2,6,1]
Type: List PrimeField 17
(4) -> u: R := 2
(4) 2
Type: PrimeField 17
(5) -> [u^i for i in 0..16]
(5) [1,2,4,8,16,15,13,9,1,2,4,8,16,15,13,9,1]
Type: List PrimeField 17
The first list shows that 3 is a primitive 16-th root of unity.
However with
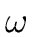 = 2 we have
= 2 we have
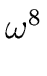 - 1 = 0
since
(24 - 1)(24 + 1) = 15×17
- 1 = 0
since
(24 - 1)(24 + 1) = 15×17  0.
0.
Lemma 1
Let
1 <
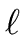
<
n be integers and let
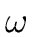
be a primitive
n-th
root of unity. Then we have
-
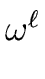 - 1 is neither zero nor a zero divisor in R,
- 1 is neither zero nor a zero divisor in R,
-
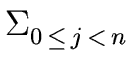
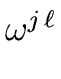 = 0.
= 0.
Proof.
It relies on the formula
(c - 1) 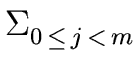 cj = cm - 1 cj = cm - 1 |
(5) |
which holds for every
c 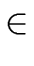 R
R and every positive integer
m.
Let us prove the first statement of the lemma.
Let g be the gcd of 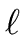 and n.
Let
u, v
and n.
Let
u, v 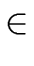
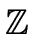 be such that
be such that
u 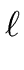 + v n = g + v n = g |
(6) |
Since
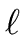
<
n we have
1
 g
g <
n.
Hence we can cancel a prime factor
t of
n such that
Let
c = 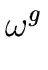 and m = n/(tg) and m = n/(tg) |
(8) |
in Relation (
5) leading to
(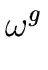 - 1) a = ( - 1) a = (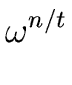 - 1) - 1) |
(9) |
for some
a 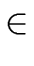 R
R.
Hence if
(
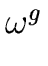
- 1) would be zero or a zero divisor
then so would be
(
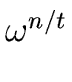
- 1) which is false.
Now applying Relation (
5) with
c =
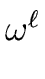
and
m =
u implies that
(
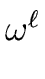
- 1) divides
(
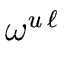
- 1).
But with Relation (
6) we obtain
(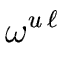 - 1) = ( - 1) = (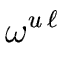 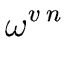 - 1) = ( - 1) = (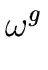 - 1) - 1) |
(10) |
Hence
(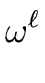 - 1) | ( - 1) | (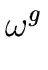 - 1) - 1) |
(11) |
Therefore
(
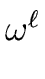
- 1) cannot be zero or a zero divisor.
Now let us prove the second statement of the lemma.
By applying Relation (5)
with
c = 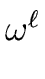 and m = n we have
and m = n we have
Since
(
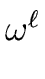
- 1) is neither zero nor a zero divisor we otain
the desired formula.



Next: The Discrete Fourier Transform
Up: Fast Polynomial Multiplication based on
Previous: Fast Polynomial Multiplication based on
Marc Moreno Maza
2003-06-06
![]() R is a zero divisor
if a
R is a zero divisor
if a ![]() 0 and there exists b
0 and there exists b ![]() R such that
a b = 0 and b
R such that
a b = 0 and b ![]() 0.
0.
![]()
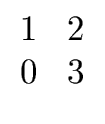
![]() is nonsingular but has no inverse (right or left).
But this is not a good example since we limit ourselves
to commutative rings. So consider instead the following example.
is nonsingular but has no inverse (right or left).
But this is not a good example since we limit ourselves
to commutative rings. So consider instead the following example.
![]() [x] where
[x] where ![]() is a field and the residue class ring
is a field and the residue class ring
![]() /m
/m![]() (with m > 1 not necessarily prime).
The ring
(with m > 1 not necessarily prime).
The ring
![]() [x] has no zero divisors
whereas
[x] has no zero divisors
whereas
![]() /m
/m![]() has zero divisors iff m is not prime.
But for every non prime m the ring
has zero divisors iff m is not prime.
But for every non prime m the ring
![]() /m
/m![]() consists only of zero, units and zero divisors.
This follows from the proposition below.
This is why we were led to the
consists only of zero, units and zero divisors.
This follows from the proposition below.
This is why we were led to the
![]() /6
/6![]() [x] example.
[x] example.
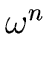 = 1.
= 1.
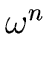 = 1,
= 1,
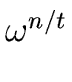 - 1
is neither zero nor a zero divisor.
- 1
is neither zero nor a zero divisor.
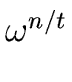
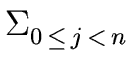
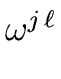 = 0.
= 0.
![]() and n.
Let
u, v
and n.
Let
u, v ![]()
![]() be such that
be such that
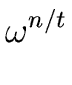 - 1)
- 1)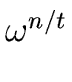 - 1) which is false.
Now applying Relation (5) with
c =
- 1) which is false.
Now applying Relation (5) with
c = 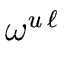 - 1).
But with Relation (6) we obtain
- 1).
But with Relation (6) we obtain
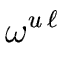 - 1) = (
- 1) = (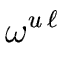
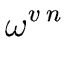 - 1) = (
- 1) = (![]() and m = n we have
and m = n we have
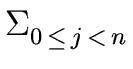
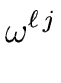 =
= 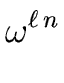 - 1 = 0
- 1 = 0