Proof.
It is sufficient to see that
| f * |1 | w|1 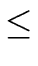 B and | g * |1 | w|1 B and | g * |1 | w|1 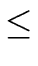 B B |
(99) |
both hold iff
normal(
pp(w)) =
h.
If the conditions hold then
| f * w| 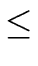 | f * w|1 | f * w|1 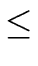 | f * |1 | w|1 | f * |1 | w|1 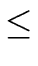 B < p/2 B < p/2 |
(100) |
Moreover from the algorithm computations we have
| b f|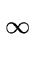 < p/2 < p/2 |
(101) |
and
f * w  b f modp b f modp |
(102) |
Relations (
100) and (
101) imply
that every coefficient
c of
f * w -
b f
satisfies
-
p <
c <
p.
Whereas Relation (
102) tells us that
every coefficient
c of
f * w -
b f
is a multiple of
p.
Therefore we have
Similarly we have
This implies that
w divides
gcd(
b f,
b g).
Hence the primitive part of
w divides that of
gcd(
b f,
b g)
which is
h.
On the other hand
- w and
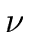 have the same degree since
w
have the same degree since
w  b
b 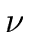 modp
holds and since p does not divide b.
modp
holds and since p does not divide b.
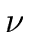 has degree equal or greater to that of h by virtue of
Theorem 3.
has degree equal or greater to that of h by virtue of
Theorem 3.
Therefore
pp(
w) and
h have the same degree and are in fact equal
up to a sign.
Conversely assume that
normal(
pp(w)) is
h.
Recall that
w and
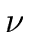
have the same degree.
Then the polynomials
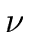
and
h have the same degree too.
Hence by virtue of Theorem
3
we have
where
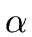
=
lc(
h).
Since
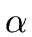
divides
b let
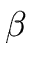
be such that
b =
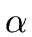
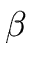
.
Hence we have
Now by construction we have
| w|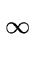 < p/2 < p/2 |
(107) |
Moreover Corollary
4 states that
| h|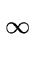  (n + 1)1/2 2n | f| (n + 1)1/2 2n | f|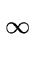 |
(108) |
which implies
Relations (
105), (
106) and (
107) imply
w = 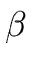 h h |
(110) |
Since
h divides
f and
g we deduce from Relation (
109) that
w divides
b f and
b g.
Hence there exist polynomials
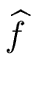
and
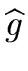
such that
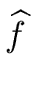 w = b f and w = b f and 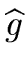 w = b g w = b g |
(111) |
Corollary
4 applied to
(
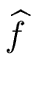
,
w) (as factors of
b f)
and
(
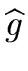
,
w) (as factors of
b g) shows to
|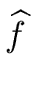 |1 | w|1 |1 | w|1 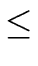 B and | B and |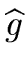 |1 | w|1 |1 | w|1 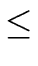 B B |
(112) |
Finally, it follows from the way
f * and
g * are computed that we have in fact
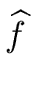 = f * and = f * and 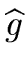 = g * = g * |
(113) |
and we proved that Relation (
99)
holds!

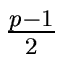 ,
,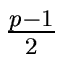 ]
]