Next: The Discrete Fourier Transform Up: Fast Polynomial Multiplication based on Previous: Fast Polynomial Multiplication based on
Let us recall that an element 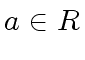 is a zero divisor
if
is a zero divisor
if 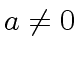 and there exists
and there exists 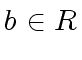 such that
such that
![]() and
and 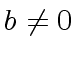 .
.
Let us recall also that because the ring ![]() has a unit
has a unit ![]() then there is a map
then there is a map
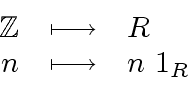 |
(1) |
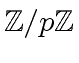 .
.
Observe also the ring ![]() may contain nonzero elements that are neither
zero divisor, nor units. For instance in the ring of square
matrices of order 2 with integer coefficients the matrix
may contain nonzero elements that are neither
zero divisor, nor units. For instance in the ring of square
matrices of order 2 with integer coefficients the matrix
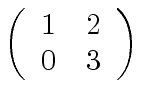 is nonsingular but has no inverse (right or left).
But this is not a good example since we limit ourselves
to commutative rings. So consider instead the following example.
is nonsingular but has no inverse (right or left).
But this is not a good example since we limit ourselves
to commutative rings. So consider instead the following example.
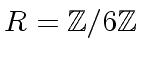 and let
and let ![$ U = R[x]$](img32.png) be
the ring of univariate polynomials over
be
the ring of univariate polynomials over 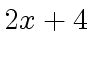 since
since
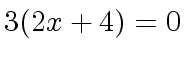 ) and also
elements like
) and also
elements like 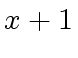 which is not a unit nor
a zero divisor.
which is not a unit nor
a zero divisor.
Why do we need to take such exotic examples?
Because among the rings you are familiar with, this is
the simplest example of ring having zero divisors, units
and nonzero elements that are not zero divisors or units.
Indeed our usual rings are
![$ {\bf k}[x]$](img38.png) where
where ![]() is a field and the residue class ring
is a field and the residue class ring
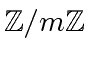 (with
(with 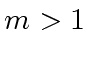 not necessarily prime).
The ring
not necessarily prime).
The ring
![$ {\bf k}[x]$](img38.png) has no zero divisors
whereas
has no zero divisors
whereas
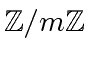 has zero divisors iff
has zero divisors iff ![]() is not prime.
But for every non prime
is not prime.
But for every non prime ![]() the ring
the ring
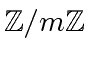 consists only of zero, units and zero divisors.
This follows from the proposition below.
This is why we were led to the
consists only of zero, units and zero divisors.
This follows from the proposition below.
This is why we were led to the
![$ {\mbox{${\mathbb{Z}}$}}/6{\mbox{${\mathbb{Z}}$}}[x]$](img43.png) example.
example.
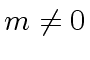 and
and 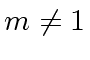 .
Consider the residue class ring
.
Consider the residue class ring
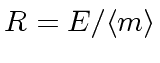 where
where
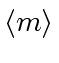 denotes the ideal generated by
denotes the ideal generated by
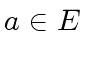 .
So let
.
So let 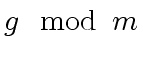 would be zero
and
would be zero
and 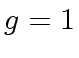 then
then
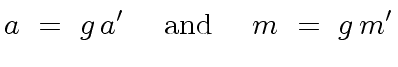 |
(3) |
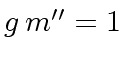 ).
We have
).
We have
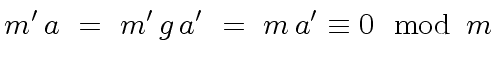 |
(4) |
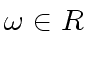 .
.
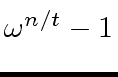 is neither zero nor a zero divisor.
is neither zero nor a zero divisor.
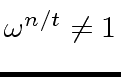 .
Observe also that a
.
Observe also that a
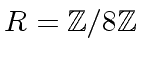 we have
we have
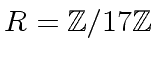 we have the following computation in AXIOM
we have the following computation in AXIOM
(1) -> R := PF(17)
(1) PrimeField 17
Type: Domain
(2) -> w: R := 3
(2) 3
Type: PrimeField 17
(3) -> [w^i for i in 0..16]
(3) [1,3,9,10,13,5,15,11,16,14,8,7,4,12,2,6,1]
Type: List PrimeField 17
(4) -> u: R := 2
(4) 2
Type: PrimeField 17
(5) -> [u^i for i in 0..16]
(5) [1,2,4,8,16,15,13,9,1,2,4,8,16,15,13,9,1]
Type: List PrimeField 17
The first list shows that 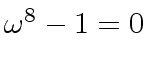 since
since
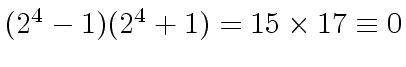 .
.
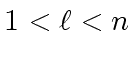 be integers and let
be integers and let 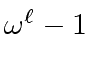 is neither zero nor a zero divisor in
is neither zero nor a zero divisor in 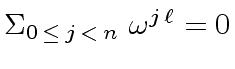 .
.
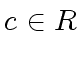 and every positive integer
and every positive integer
Let us prove the first statement of the lemma.
Let ![]() be the gcd of
be the gcd of ![]() and
and ![]() .
Let
.
Let
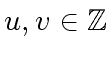 be such that
be such that
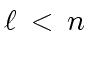 we have
we have
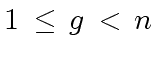 .
Hence we can cancel a prime factor
.
Hence we can cancel a prime factor 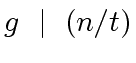 |
(7) |
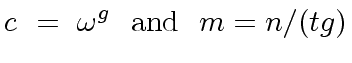 |
(8) |
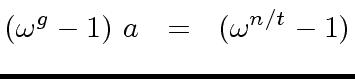 |
(9) |
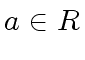 .
Hence if
.
Hence if
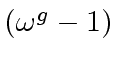 would be zero or a zero divisor
then so would be
would be zero or a zero divisor
then so would be
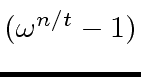 which is false.
Now applying Relation (5) with
which is false.
Now applying Relation (5) with
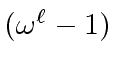 divides
divides
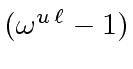 .
But with Relation (6) we obtain
.
But with Relation (6) we obtain
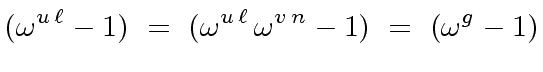 |
(10) |
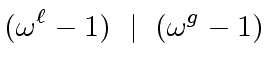 |
(11) |
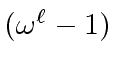 cannot be zero or a zero divisor.
cannot be zero or a zero divisor.
Now let us prove the second statement of the lemma.
By applying Relation (5)
with
![]() and
and ![]() we have
we have
 |
(12) |
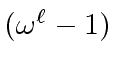 is neither zero nor a zero divisor we otain
the desired formula.
is neither zero nor a zero divisor we otain
the desired formula.
Marc Moreno Maza