Next: Convolution of polynomials Up: Fast Polynomial Multiplication based on Previous: Primitive roots of unity
Let ![]() be a positive integer and
be a positive integer and
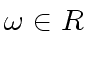 be a primitive
be a primitive ![]() -th
root of unity.
In what follows we identify every univariate polynomial
-th
root of unity.
In what follows we identify every univariate polynomial
![$\displaystyle f \ = \ {\Sigma}_{0 \, \leq \, i \, < \, n} \ f_i \, x^i \ \in R[x]$](img108.png) |
(13) |
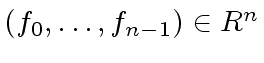 .
.
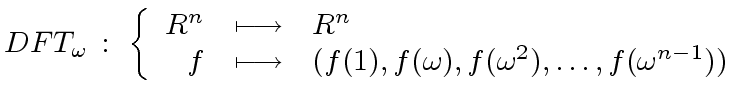 |
(14) |
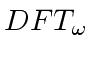 is an isomorphism.
is an isomorphism.
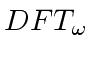 is an endomorphism
(the source and target spaces are the same)
we only need to prove
that
is an endomorphism
(the source and target spaces are the same)
we only need to prove
that
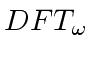 is bijective.
Observe that the Vandermonde matrix
is bijective.
Observe that the Vandermonde matrix
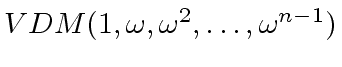 is the matrix of the
is the matrix of the 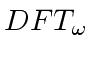 .
Then for proving that
.
Then for proving that
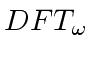 is bijective
we need only to prove that
is bijective
we need only to prove that
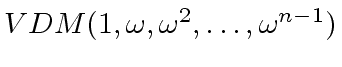 is invertible which holds iff the values
is invertible which holds iff the values
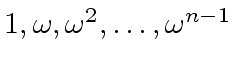 are pairwise different.
A relation
are pairwise different.
A relation
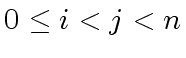 would imply
would imply
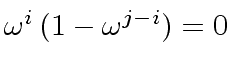 .
Since
.
Since
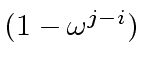 cannot be zero or a zero divisor
then
cannot be zero or a zero divisor
then
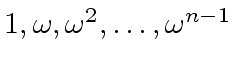 are pairwise different and
are pairwise different and
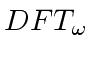 is an isomorphism.
is an isomorphism.
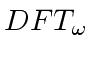 .
Then
.
Then
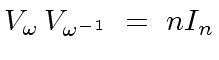 |
(15) |
Let us consider the product of the matrix
![]() and
and
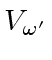 .
The element at row
.
The element at row ![]() and column
and column ![]() is
is
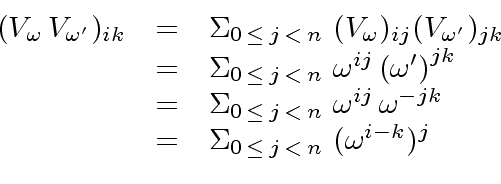 |
(16) |
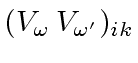 is equal to
is equal to 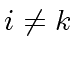 then the conclusion follows by applying the second statement of
Lemma 1
which shows that
then the conclusion follows by applying the second statement of
Lemma 1
which shows that
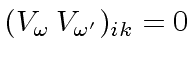 .
.
Marc Moreno Maza