Next: Computing primitive -th roots of Up: Fast Polynomial Multiplication based on Previous: The Fast Fourier Transform
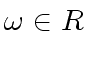 a primitive
a primitive ![$ R[x]/{{\langle} x^n - 1 {\rangle}}$](img223.png) and
multiplication in
and
multiplication in ![$ R[x]$](img137.png) of polynomials whose product has degree less than
of polynomials whose product has degree less than 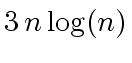 additions in
additions in 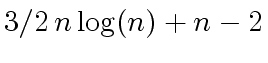 multiplications by a power of
multiplications by a power of 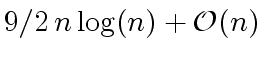 operations in
operations in
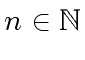 we only need a primitive
we only need a primitive 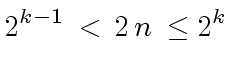 |
(41) |
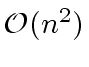 of the classical
algorithm to
of the classical
algorithm to
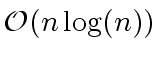 .
.
Marc Moreno Maza