mathend000#.
Next, we prove (iii)
mathend000#.
So we consider (r, t)
mathend000# a solution to
RFR(m, n, f, d )
mathend000#
such that the fraction r/t
mathend000# is in canonical form.
There exists
s 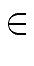
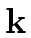 [x]
mathend000# such that we have
r = sm + tf
mathend000#.
Since
degr + degt < degm
mathend000# holds,
we can apply Proposition 3.
So, let
[x]
mathend000# such that we have
r = sm + tf
mathend000#.
Since
degr + degt < degm
mathend000# holds,
we can apply Proposition 3.
So, let
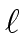
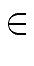 {1,..., k + 1}
mathend000# be such that
{1,..., k + 1}
mathend000# be such that
Then, there exists
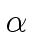
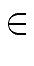
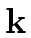 [x]
mathend000# such that
r =
[x]
mathend000# such that
r = 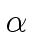 r
r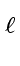 mathend000# and
t =
mathend000# and
t = 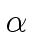 t
t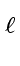 mathend000# both hold.
mathend000# both hold.
If
degrj 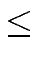 degr
mathend000# then we have
degr
mathend000# then we have
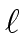 = j
mathend000#.
If
degr < degrj
mathend000# then we have
= j
mathend000#.
If
degr < degrj
mathend000# then we have
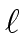 > j
mathend000#.
> j
mathend000#.
We prove that
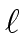 = j
mathend000# holds.
If t = tj
mathend000# then
r - rj
= j
mathend000# holds.
If t = tj
mathend000# then
r - rj  0 modm
mathend000#,
and thus r = rj
mathend000#, since
deg(r - rj) < n
mathend000# holds,
which implies
0 modm
mathend000#,
and thus r = rj
mathend000#, since
deg(r - rj) < n
mathend000# holds,
which implies
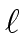 = j
mathend000#.
If
t
= j
mathend000#.
If
t 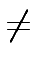 tj
mathend000#, we can apply Proposition 3
again.
Then, there exists
tj
mathend000#, we can apply Proposition 3
again.
Then, there exists
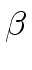
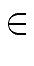
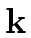 [x]
mathend000# such that
r - rj =
[x]
mathend000# such that
r - rj = 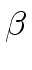 r
r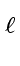 mathend000# and
t - tj =
mathend000# and
t - tj = 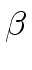 t
t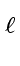 mathend000# both hold.
It follows that we have
rj = (
mathend000# both hold.
It follows that we have
rj = (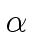 -
- 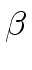 )r
)r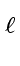 mathend000#
and
tj = (
mathend000#
and
tj = (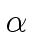 -
- 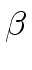 )t
)t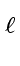 mathend000#.
Hence, we deduce
mathend000#.
Hence, we deduce
msj = rj - tjf = (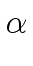 - - 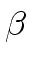 )ms )ms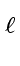 |
(94) |
leading to
sj = (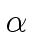 -
- 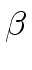 )s
)s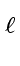 mathend000#.
Since
gcd(sj, tj) = 1
mathend000# holds
we must have
mathend000#.
Since
gcd(sj, tj) = 1
mathend000# holds
we must have
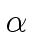 -
- 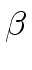
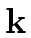 mathend000#
and thus
rj = r
mathend000#
and thus
rj = r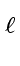 mathend000#.
Therefore, we have proved that
mathend000#.
Therefore, we have proved that
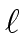 = j
mathend000# holds.
This implies
= j
mathend000# holds.
This implies
r = 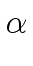 rj and t = rj and t = 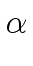 tj tj |
(95) |
Since r/t
mathend000# is in canonical form, we deduce that
gcd(tj, rj) = 1
mathend000# and
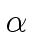 = (lc(tj))-1
mathend000# hold.
This proves (iii)
mathend000#.
Finally, (iv)
mathend000# follows from (ii)
mathend000# and (iii)
mathend000#.
= (lc(tj))-1
mathend000# hold.
This proves (iii)
mathend000#.
Finally, (iv)
mathend000# follows from (ii)
mathend000# and (iii)
mathend000#.

![]()
![]()
![]() [x]
[x]
![]()
![]() [x]
[x]
![]() {1,..., n}
{1,..., n}
![]()
![]() (x)
(x)
![]()
![]() [x]
[x]
![]()
![]() (x)
(x)
![]()
![]() [x]
[x]
![]()
![]() {1,..., k + 1}
{1,..., k + 1}
![]()
![]() degr < degr
degr < degr![]() -1.
-1.![]()
![]()
![]() [x]
[x]
![]() r
r![]()
![]() t
t![]()
![]() degr
degr
![]() = j
= j
![]() > j
> j
![]() = j
= j
![]() 0 modm
0 modm
![]() = j
= j
![]() tj
tj
![]()
![]()
![]() [x]
[x]
![]() r
r![]()
![]() t
t![]()
![]() -
- ![]() )r
)r![]()
![]() -
- ![]() )t
)t![]()
![]() -
- ![]() )ms
)ms![]()
![]() -
- ![]() )s
)s![]()
![]() -
- ![]()
![]()
![]()
![]()
![]() = j
= j
![]() rj and t =
rj and t = ![]() tj
tj![]() = (lc(tj))-1
= (lc(tj))-1
![]()