THE METHOD.
a 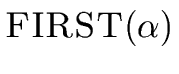  ( ( a a |
(40) |
So match(a) moves the cursor lookahead one symbol forward iff lookahead points to a. Otherwise an error is produced.
In other words, given a nonterminal A the call proc
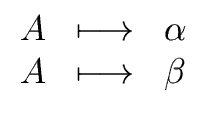 |
(41) |
| S |
|
cAd |
| A |
|
ab | a |
| type |
|
simple | |
| simple |
|
integer | char | num dotdot num |
| FIRST(simple) | = | { integer, char, num } |
|
FIRST( |
= | { |
| FIRST(array[simple] of type) | = | { array } |
| FIRST(integer) | = | { integer } |
| FIRST(char) | = | { char } |
| FIRST(num dotdot num) | = | { num } |