Remark 1
Let I be a finite set of identifiers and let us consider
the alphabet
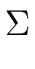 = I = I 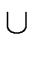 { + , - ,*,/, { + , - ,*,/, 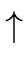 ,(,)}. ,(,)}. |
(1) |
Let L be the language consisting of arithmetic expressions
over 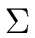 .
We shall show that L cannot be recognized by FA.
.
We shall show that L cannot be recognized by FA.
First we observe that every word
w = w1 ... w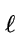 of L
is a well parenthesized expression that is
of L
is a well parenthesized expression that is
( i = 1 ... i = 1 ... 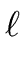 - 1) | w1 ... wi - 1) | w1 ... wi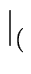 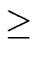 | w1 ... wi | w1 ... wi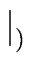 and | w and | w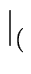 = | w = | w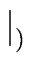 |
(2) |
where
| u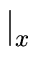 denotes the number of occurrences
of the letter x in the word u.
The proof is easy by induction.
denotes the number of occurrences
of the letter x in the word u.
The proof is easy by induction.
Let us assume that L can be recognized by a DFA
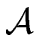 = (
= (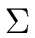 , S, s0, F,
, S, s0, F,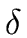 )
with N states and initial state s0.
Let us consider an arithmetic expression a starting with N opening
parentheses. There exists N states
s1, s2,..., sN such that
for every
i = 1 ... N - 1 we have
)
with N states and initial state s0.
Let us consider an arithmetic expression a starting with N opening
parentheses. There exists N states
s1, s2,..., sN such that
for every
i = 1 ... N - 1 we have
si+1 = 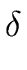 (si, x) with x = ( (si, x) with x = ( |
(3) |
There exists at least two values i1 and i2 of the index i
in the range
0 ... N such that
si1 = si2.
Hence by adding i2 - i1 opening parentheses in front of a
we can build another word b recognized by L.
However b is clearly not a well parenthesized expression
and thus it is not an arithmetic expression.
Figure 1:
Well parenthesized expressions cannot be recognized by FA.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.5]{wellBalancedExpressions.eps}
\end{figure}](img18.png) |
Therefore the language of arithmetic expressions over 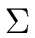 cannot be recognized by FA.
cannot be recognized by FA.
![]() of L
is a well parenthesized expression that is
of L
is a well parenthesized expression that is
![]() = (
= (![]() , S, s0, F,
, S, s0, F,![]() )
with N states and initial state s0.
Let us consider an arithmetic expression a starting with N opening
parentheses. There exists N states
s1, s2,..., sN such that
for every
i = 1 ... N - 1 we have
)
with N states and initial state s0.
Let us consider an arithmetic expression a starting with N opening
parentheses. There exists N states
s1, s2,..., sN such that
for every
i = 1 ... N - 1 we have