Proof.
Since


(
g) is invertible modulo
p
then


(
g) is invertible modulo
p2.
(This is easy to check: Exercise!)
Hence Relation
111 makes sense.
In fact, Algorithm
6
computes


(
g)
-1mod
p2
given


(
g)
-1mod
p.
Since p divides p2, the following congruence holds
h  g - g -  (g) (g)   (g)-1modp (g)-1modp |
(112) |
Since

(
g)
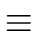
0 mod
p, this leads to
h  g modp g modp |
(113) |
and we have proved the second claim.
Let us prove the first one.
Using the Taylor expansion of

at
h
and the fact that
p2 divides (
h -
g)
2 we obtain
 (h) (h) |
 |
 (g) + (g) +   (g)(h - g)modp2 (g)(h - g)modp2 |
| |
 |
 (g) - (g) -   (g) (g) (g) (g)   (g)-1modp2 (g)-1modp2 |
| |
 |
0 modp2 |
|
(114) |
proving the first claim.
Finally, observe that
h 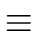 g
g mod
p implies


(
h)
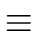


(
g)mod
p.
Indeed


is a polynomial in
R[
x].
Therefore,


(
h) is invertible modulo
p,
since


(
g) is invertible modulo
p, by hypothesis.

Proof.
Let
gr 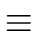 gr-1
gr-1 -

(
gr-1)
sr-1mod
p2r.
Then we have
g  gr modp gr modp |
(116) |
In other words
gr is a
solution of higher precision.
Then proving the theorem turns into proving the invariants for
i = 0
... r
-
gi
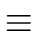 g0modp,
g0modp,
-
 (gi)
(gi) 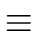 0 modp2i,
0 modp2i,
- if i < r then
si

 (gi)
(gi) 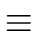 1 modp2i.
1 modp2i.
The case
i = 0 is clear and we assume that
i > 0 holds.
Then by induction hypothesis
p2i-1 divides

(
gi-1) and
si-1 -


(
gi-1)
-1.
Then
p2i divides their product, that is
 (gi-1)si-1 (gi-1)si-1   (gi-1) (gi-1)  (gi-1)-1 modp2i. (gi-1)-1 modp2i. |
(117) |
Now we calculate
| gi |
 |
gi-1 -  (gi-1)si-1 modp2i (gi-1)si-1 modp2i |
| |
 |
gi-1 -  (gi-1) (gi-1)  (gi-1)-1 modp2i (gi-1)-1 modp2i |
|
(118) |
Now applying Proposition
15
with
g =
gi-1,
h =
gi and
m =
p2i-1
we obtain the first two invariants.
In addition, this leads to
gi  gi-1 modp2i-1 gi-1 modp2i-1 |
(119) |
for
i <
r.
This implies
  (gi)-1 (gi)-1    (gi-1)-1 (gi-1)-1  si-1 modp2i-1 si-1 modp2i-1 |
(120) |
Now,
si is obtained by one Newton step for inversion
(see Algorithm
6).
Therefore the third invariant follows.

![]() R and
R and
![]()
![]() R[y].
We are concerned with solving the equation
R[y].
We are concerned with solving the equation
![]()