

Next: Relation between gcds in [x]
Up: Advanced Computer Algebra: The resultant
Previous: Advanced Computer Algebra: The resultant
We saw in the first chapter that running the Euclidean
Algorithm in
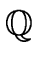 [x] can lead to a significant expression swell.
Let us try to estimate how coefficients grow.
That is, we want to estimate the maximal space
needed to store one coefficient of an intermediate polynomial.
Let N be the number of bits of a machine word.
[x] can lead to a significant expression swell.
Let us try to estimate how coefficients grow.
That is, we want to estimate the maximal space
needed to store one coefficient of an intermediate polynomial.
Let N be the number of bits of a machine word.
Definition 1
For an integer
a 
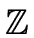
we define
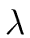
(
a) the
length of
a as the minimum number of words to encode
a.
Hence for
a 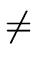
0 we have
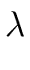 (a) = (a) =  log2(a)/N log2(a)/N + 1 and + 1 and 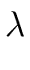 (0) = 0 (0) = 0 |
(1) |
For a rational number
a =
b/
c with
b,
c 
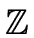
and
gcd(
c,
d )= 1
we define
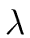
(
a), the
length of
a, as the maximum
among
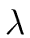
(
b) and
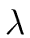
(
c).
Definition 2
For a polynomial
a 
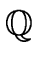
[
x] of degree
n 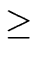
0
such that all coefficients have denominator
b and such that the
numerators
an,
an-1,...,
a1,
a0 have gcd 1
then we define the
length of
a as
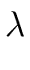 (a) = max( (a) = max(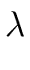 (b), (b),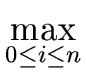 ( (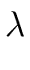 (ai))) (ai))) |
(2) |
Remark 1
A polynomial
a 
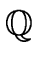 [x] of degree n
[x] of degree n 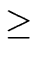 0
can be represented with
words.
0
can be represented with
words.
Proposition 2
Let
a,
b be univariate polynomials over
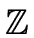
in
x.
We assume that
a and
b are monic and that
deg(
a) = deg(
b) + 1 holds.
Let
q and
r be the quotient and the remainder of
a w.r.t.
b.
Then we have
Proof.
We define
| a = xn + an-1xn-1 + ... + a0 and b = xn-1 + bn-2xn-2 + ... + b0 |
(5) |
It is not hard to see that
Then
Thus
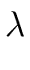 (bq) (bq) 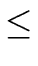 max( max(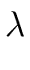 (a), (a),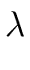 (b)) + 1 + (b)) + 1 + 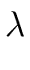 (b) + (b) + 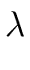 (deg(q) + 1) (deg(q) + 1) |
(8) |
Recall that
Since
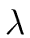
(
bq)
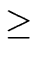
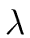
(
a) we obtain
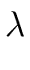 (r) (r) |
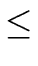 |
max(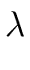 (a), (a),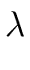 (b)) + 1 + (b)) + 1 + 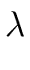 (b) + (b) + 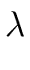 (deg(q) + 1) + 1 (deg(q) + 1) + 1 |
| |
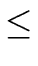 |
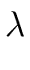 (a) + 2 (a) + 2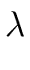 (b) + 3 (b) + 3 |
|
(10) |
Indeed
max(
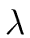
(
a),
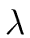
(
b))
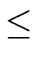
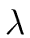
(
a) +
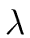
(
b)
and
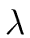
(deg(
q) + 1) =
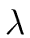
(2)
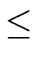
1.

Remark 2
A similar result as Proposition 2
holds for monic polynomials
a, b 
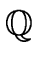 [x] such that
deg(a) = deg(b) + 1.
See [vzGG99].
These results provide us with an exponential upper bound for the
coefficient of the gcd computed by the Euclidean Algorithm.
But in fact a polynomial bound can be established.
Moreover there is an efficient modular approach for computing gcds in
[x] such that
deg(a) = deg(b) + 1.
See [vzGG99].
These results provide us with an exponential upper bound for the
coefficient of the gcd computed by the Euclidean Algorithm.
But in fact a polynomial bound can be established.
Moreover there is an efficient modular approach for computing gcds in
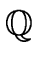 [x] and
[x] and
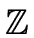 [x]
as we shall see in the next sections.
[x]
as we shall see in the next sections.


Next: Relation between gcds in [x]
Up: Advanced Computer Algebra: The resultant
Previous: Advanced Computer Algebra: The resultant
Marc Moreno Maza
2004-04-27
![]() [x] can lead to a significant expression swell.
Let us try to estimate how coefficients grow.
That is, we want to estimate the maximal space
needed to store one coefficient of an intermediate polynomial.
Let N be the number of bits of a machine word.
[x] can lead to a significant expression swell.
Let us try to estimate how coefficients grow.
That is, we want to estimate the maximal space
needed to store one coefficient of an intermediate polynomial.
Let N be the number of bits of a machine word.
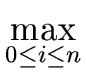 (
(