

Next: The resultant
Up: Advanced Computer Algebra: The resultant
Previous: Coefficients growth in the Euclidean
Notation 1
Let R be a commutative ring with identity element.
Every element a  R can be written
where
normal
R can be written
where
normal(
a) stands for a canonical representative
of the class of the elements associate with
a
and where
lu(
a) is a unit.
Observe that
a is a unit iff
normal(
a) is 1.
For
R = 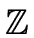 we will take
normal(a) = | a |.
For
R =
we will take
normal(a) = | a |.
For
R = 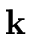 [x] we will take
normal(a) = a/lc(a).
[x] we will take
normal(a) = a/lc(a).
Definition 3
Let
R be a UFD and
f =
fnxn +
... +
f1x +
f0
be a univariate polynomial over
R of positive degree.
The
content of
f, denoted
cont(
f )
is the gcd of its coefficients
fn,...,
f1,
f0.
By convention the content of a constant polynomial
f0  R
R
is
normal(
f0).
Observe that
cont(
f ) is uniquely defined in any case.
The polynomial
f  R[x] is primitive if
cont(f )= 1.
The primitive part of
f
R[x] is primitive if
cont(f )= 1.
The primitive part of
f  R[x] is the polynomial
pp(f )
R[x] is the polynomial
pp(f )  R[x] such that
R[x] such that
Proposition 3
If
R is a UFD, for
f  R
R[
x] and
c  R
R we have
| cont(c f ) = c cont(f ) and pp(c f ) = c pp(f ) |
(15) |
Theorem 1 (Gauss Lemma)
If R is a UFD, the product of two primitive polynomials
in R[x] is primitive.
Proof.
Let
R be a UFD.
Let
f,
g  R
R[
x] be primitive.
Let
p  R
R be a prime.
Then, the residue class ring
D =
R/
p is an integral domain.
It follows (this is a classical result) that
D[
x] is an integral domain too.
By hypothesis
f mod
p and
g mod
p are not zero.
Hence
fg mod
p is not zero too.
This shows that
p cannot divide
cont(
fg).
Finally we have proved that no primes divide
cont(
fg)
and thus
cont(
fg) = 1.

Corollary 1
Let
R be a UFD.
Let
f,
g  R
R[
x].
Then we have
| cont(fg) = cont(f ) cont(g) and pp(fg) = pp(f ) pp(g). |
(16) |
Proof.
Let
h =
pp(
fg) and
h * =
pp(
f )
pp(
g).
By Gauss Lemma, the polynomial
h * is primitive.
By definition of the content and the primitive part of a polynomial, we have
| fg |
= |
cont(f ) pp(f ) cont(g) pp(g) |
| |
= |
cont(f ) cont(g) h * . |
|
(17) |
Then since
h * is primitive,
with Proposition
3,
we get
| cont(fg) |
= |
cont(cont(f ) cont(g) h * ) |
| |
= |
cont(f ) cont(g). |
|
(18) |

Theorem 2 (Gauss)
If
R is a UFD, then so is
R[
x].
Corollary 2
Let
R be
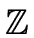
or a field.
Then
R[
x1,...,
xn] is a UFD.
Proof.
This is a direct consequence of Theorem
2.

Corollary 3
Let
R be a UFD with field of fractions
K.
Let
f,
g  R
R[
x] be univariate polynomials over
R
and let
h be their normalized gcd in
R[
x].
Then the following properties hold.
- The prime elements of R[x] are the primes of R
plus the primitive polynomials in R[x] that are irreducible in K[x].
-
cont(h) = gcd(cont(f ), cont(g)) in R.
-
pp(h) = gcd(pp(f ), pp(g)) in R[x].
-
h = gcd(cont(f ), cont(g)) gcd(pp(f ), pp(g))
-
h/lc(h) is the monic gcd of f and g in K[x].
Remark 5
From Corollary 3
we can derive an algorithm for computing
the normalized gcd h of
f, g  R[x] by means of a polynomial gcd computation
in K[x] and gcd computations in R.
We define
R[x] by means of a polynomial gcd computation
in K[x] and gcd computations in R.
We define
| c = gcd(cont(f ), cont(g)) |
(19) |
To compute the primitive part of
![$ \gcd_{{{R[x]}}}^{{}}$](img20.png) (f, g) we can assume that
f and g are divided out by their contents.
Let
(f, g) we can assume that
f and g are divided out by their contents.
Let 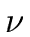 be the monic gcd of f and g in K[x].
We have
be the monic gcd of f and g in K[x].
We have
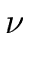 = h/lc(h) = h/lc(h) |
(20) |
Since h divides f and g in R[x]
then
lc(
h) divides
lc(
f ) and
lc(
g) in
R.
Hence
lc(
h) divides
gcd(
lc(
f ),
lc(
g)).
We define
| b = gcd(lc(f ), lc(g)) |
(21) |
Since
h = lc(
h)
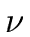
lies in
R[
x]
and since
lc(
h) divides
b we have
b 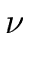 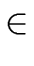 R[x] R[x] |
(22) |
Finally we obtain
h = c pp(b 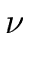 ) ) |
(23) |


Next: The resultant
Up: Advanced Computer Algebra: The resultant
Previous: Coefficients growth in the Euclidean
Marc Moreno Maza
2004-04-27
![]() [x] to
[x] to
![]() [x]
we should be careful.
For instance with
[x]
we should be careful.
For instance with
![]() we will take
normal(a) = | a |.
For
R =
we will take
normal(a) = | a |.
For
R = ![]() [x] we will take
normal(a) = a/lc(a).
[x] we will take
normal(a) = a/lc(a).
![]() R[x] is primitive if
cont(f )= 1.
The primitive part of
f
R[x] is primitive if
cont(f )= 1.
The primitive part of
f ![]() R[x] is the polynomial
pp(f )
R[x] is the polynomial
pp(f ) ![]() R[x] such that
R[x] such that
![$ \gcd_{{{R[x]}}}^{{}}$](img20.png) (f, g) we can assume that
f and g are divided out by their contents.
Let
(f, g) we can assume that
f and g are divided out by their contents.
Let ![]() [x] (and more generally
over
[x] (and more generally
over
![]() [x1,..., xn]) the modular methods (to be described
shortly) are much more efficient than going through
[x1,..., xn]) the modular methods (to be described
shortly) are much more efficient than going through
![]() [x]
and the Euclidean Algorithm.
[x]
and the Euclidean Algorithm.