

Next: Non-deterministic Finite Automata
Up: Finite Automata
Previous: Finite Automata
ALPHABET, STRING, LANGUAGE. We call an alphabet any finite set of symbols.
Let  be an alphabet.
A string or word over
be an alphabet.
A string or word over  is any finite sequence
of symbols from
is any finite sequence
of symbols from  .
The empty string is denoted by
.
The empty string is denoted by
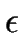 .
A language over
.
A language over  is any set of strings over
is any set of strings over  .
Note that the above definitions do not ascribe any meaning
to the strings of the language.
.
Note that the above definitions do not ascribe any meaning
to the strings of the language.
DETERMINISTIC FINITE AUTOMATA. A deterministic finite automaton (DFA) consists of five things:
- an input alphabet
 ,
,
- a finite set S whose elements are called states,
- a distinguished state
s0
 S, called starting state,
S, called starting state,
- a set
F
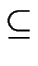 S of distinguished states, called accepting states (or final states),
S of distinguished states, called accepting states (or final states),
- a partial function
 from
S×
from
S× to S called the transition function
(hence for every state-symbol couple either
to S called the transition function
(hence for every state-symbol couple either
 maps it to a symbol or
maps it to a symbol or
 is not defined for this couple).
is not defined for this couple).
It is convenient
- to say ``let
 = (
= ( , S, s0, F,
, S, s0, F, )
be a DFA'' for ``let
)
be a DFA'' for ``let  be a DFA with alphabet
be a DFA with alphabet  ,
set of states S, starting state s0, set of accepting states F
and transition function
,
set of states S, starting state s0, set of accepting states F
and transition function  .``
.``
- to represent a DFA by a transition diagram
using the rules shown on Figure 1.
Figure 1:
Pictorial notations for finite automata.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.5]{automataNotation.eps}
\end{figure}](img8.png) |
LANGUAGE RECOGNIZED BY A DFA. A DFA accepts an input string if when beginning the computation
in the starting state, after reading the entire string, the
automaton is in an accepting state.
Figure 2:
Some finite automata accepting some lexical tokens.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.4]{4automatas.eps}
\end{figure}](img9.png) |
The set of the strings recognized by a DFA  is called
the language recognized by the DFA
is called
the language recognized by the DFA  and will be denoted by
and will be denoted by
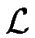 (
( ).
).
TRANSITION TABLE. A straightforward way to implement a DFA is to represent
the transition function  as a transition table.
This table has a row for each state s and a column for
each input symbol a .
The intersection of row s and column a contains
as a transition table.
This table has a row for each state s and a column for
each input symbol a .
The intersection of row s and column a contains
 (s, a).
Figure 3 shows the transition diagram
and the transition table of an automaton.
(s, a).
Figure 3 shows the transition diagram
and the transition table of an automaton.
Figure 3:
Transition table for a DFA.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.4]{transitionTable.eps}
\end{figure}](img11.png) |
A DFA can be easily converted to a program
to look for tokens specified by it.
COMPLETE DFA. A DFA
 = (
= ( , S, s0, F,
, S, s0, F, )
is said complete if for every s
)
is said complete if for every s  S and for
every
a
S and for
every
a 
 the transition
the transition
 (s, a)
is defined.
(s, a)
is defined.
The automaton of Figure 3 is complete
whereas none of the automata of Figure 2 are.
As a model for a computer program, it is desirable for a DFA
to be complete.
To transform a non-complete DFA
 = (
= ( , S, s0, F,
, S, s0, F, )
into a complete DFA one needs only
)
into a complete DFA one needs only
- to add a new state to S, say E
(for error) and then
- for every
(s, a)
 S×
S× such that
such that  was not defined
at this couple, define
was not defined
at this couple, define
 (s, a) = E.
(s, a) = E.
DFA RECOGNIZING THE UNION OF SEVERAL LANGUAGES. Each of the four DFA in Figure 2
recognizes a simple language over the alphabet
Let us denote these languages by
L1, L2, L3, L4.
- L1 is the language reduced to the single world if,
- L2 is the language of the identifiers made from
letters and digits and starting with a letter,
- L3 is the language of the integer numbers,
- L4 is the language of the floating point numbers.
It is desirable to build a DFA that would recognize
the language
L1  L2
L2  L3
L3  L4.
In other words, one would like to combine the four
transition diagrams in Figure 2
specifying the various patterns into a single
transition diagram.
This is a non-trivial task. Here are some difficulties.
L4.
In other words, one would like to combine the four
transition diagrams in Figure 2
specifying the various patterns into a single
transition diagram.
This is a non-trivial task. Here are some difficulties.
- Consider a word wi which belongs to some Li and
a word
wj
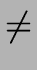
 such that wiwj belongs to some Lj.
For instance with wi = 123 and
wj = .456
should the combined DFA accept wi or wiwj?
The rule is to choose the longest initial substring
that can match a pattern (think of integers).
Hence wiwj is chosen.
such that wiwj belongs to some Lj.
For instance with wi = 123 and
wj = .456
should the combined DFA accept wi or wiwj?
The rule is to choose the longest initial substring
that can match a pattern (think of integers).
Hence wiwj is chosen.
- It may happen that wiwj (the longest match) belongs to
several Lj.
Hence we need to define some priorities.
For instance the word if belongs to L1 and L2.
However we want the word if to be a reserved word,
not an identifier.
So we have to replace L2 by
L2
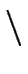 L1.
L1.
Figure 4:
An automaton
accepting
L1  L2
L2  L3
L3  L4
and solving the difficulties mentionned above.
L4
and solving the difficulties mentionned above.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.5]{1automatonFor4.eps}
\end{figure}](img16.png) |
N.B. From now on and for simplicity,
we do not consider capital letters
any more in our example (Figure 2).
In other words we reduce  to the
union of
[a ... z],
[0 ... 9] and {.}.
to the
union of
[a ... z],
[0 ... 9] and {.}.


Next: Non-deterministic Finite Automata
Up: Finite Automata
Previous: Finite Automata
Marc Moreno Maza
2004-12-02
![]() be an alphabet.
A string or word over
be an alphabet.
A string or word over ![]() is any finite sequence
of symbols from
is any finite sequence
of symbols from ![]() .
The empty string is denoted by
.
The empty string is denoted by
![]() .
A language over
.
A language over ![]() is any set of strings over
is any set of strings over ![]() .
Note that the above definitions do not ascribe any meaning
to the strings of the language.
.
Note that the above definitions do not ascribe any meaning
to the strings of the language.
![]() as a transition table.
This table has a row for each state s and a column for
each input symbol a .
The intersection of row s and column a contains
as a transition table.
This table has a row for each state s and a column for
each input symbol a .
The intersection of row s and column a contains
![]() (s, a).
Figure 3 shows the transition diagram
and the transition table of an automaton.
(s, a).
Figure 3 shows the transition diagram
and the transition table of an automaton.
![]() = (
= (![]() , S, s0, F,
, S, s0, F,![]() )
is said complete if for every s
)
is said complete if for every s ![]() S and for
every
a
S and for
every
a ![]()
![]() the transition
the transition
![]() (s, a)
is defined.
(s, a)
is defined.
![]() = (
= (![]() , S, s0, F,
, S, s0, F,![]() )
into a complete DFA one needs only
)
into a complete DFA one needs only
![\begin{equation}
{\Sigma} \ \ = \ \ [a \cdots z] \ \cup \ [A \cdots Z] \ \cup \ [0 \cdots 9]
\ \cup \ \{. \}
\end{equation}](img12.png)