

Next: Non-deterministic Finite Automata with instantaneous
Up: Finite Automata
Previous: Deterministic Finite Automata
NON-DETERMINISTIC FINITE AUTOMATA.
A non-deterministic finite automaton (NFA) consists of five things:
- an input alphabet
 ,
,
- a finite set S whose elements are called states,
- a set
I
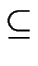 S of distinguished states, called initial states,
S of distinguished states, called initial states,
- a set
F
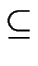 S of distinguished states, called accepting states,
S of distinguished states, called accepting states,
- a function
 from
S×
from
S× to 2S, thus every state-symbol couple
is mapped by
to 2S, thus every state-symbol couple
is mapped by  to set of states
(that is a subset of S).
to set of states
(that is a subset of S).
Observe that
- In the transition graph of a NFA the same symbol
a

 can label two or more transitions
out of one state.
can label two or more transitions
out of one state.
- Therefore after reading a given symbol, a NFA
can have several states.
LANGUAGE RECOGNIZED BY A NFA. A word w is accepted by a NFA if after reading w
the NFA is in at least one accepting state.
Figure 5 shows a NFA and a DFA
recognizing the same language: the language over
 = {a, b} consisting of the words
which end with b.
= {a, b} consisting of the words
which end with b.
Figure 5:
A NFA and a DFA accepting the same language.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.5]{DFAandNFA-1.eps}
\end{figure}](img17.png) |
FROM A NFA TO A DFA ACCEPTING THE SAME LANGUAGE.
Theorem 1
Let

= (

,
S,
I,
F,

) be a NFA
accepting the language
L.
Then there exists a DFA
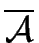
accepting
L too.
To construct such a DFA
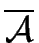 from
from  one proceeds as follows.
one proceeds as follows.
- The alphabet is unchanged.
- The set
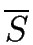 of states of
of states of
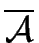 is a subset of 2S. Hence each state of
is a subset of 2S. Hence each state of
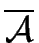 is a subset of S.
The set
is a subset of S.
The set
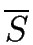 is computed by
Algorithm 1 below.
is computed by
Algorithm 1 below.
- The starting state
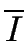 of
of
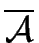 is the set I of the initial states of
is the set I of the initial states of
 .
.
- The set
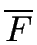 of the accepting states of
of the accepting states of
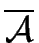 is the set of the states
is the set of the states
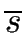 of
of
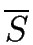 such that
such that
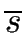
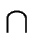 F
F 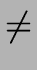
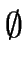 .
.
- The transition function
 of
of
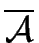 together with
together with
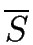 is determined by
Algorithm 1,
called the SUBSET ALGORITHM.
is determined by
Algorithm 1,
called the SUBSET ALGORITHM.
Algorithm 1
- 1
- toSee :=
[
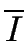 ];
];
- 2
-
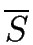 := [ ];
:= [ ];
- 3
- while
toSee
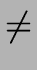 [ ] repeat
[ ] repeat
- 3.1
- A := first(toSee); toSee := rest(toSee);
- 3.2
- for
x

 repeat
repeat
- 3.2.1
-
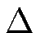 (A, x) :=
{s' | (
(A, x) :=
{s' | (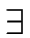 s
s  A) (s
A) (s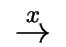 s')};
s')};
- 3.2.2
- if (
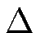 (A, x)
(A, x) 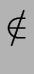 toSee) and (
toSee) and (
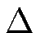 (A, x)
(A, x) 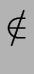
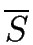 ) then toSee := cons(
) then toSee := cons(
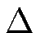 (A, x), toSee);
(A, x), toSee);
- 3.3
-
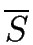 := cons(
A,
:= cons(
A,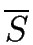 );
);
- 4
- return(
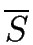 ,
,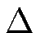 )
)
In this algorithm
- toSee is the list of the states
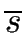 of
of
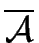 such that the
such that the
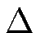 (a,
(a,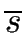 )
for all
a
)
for all
a 
 have not been computed yet,
have not been computed yet,
- whereas
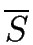 contains those states
contains those states
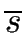 of
of
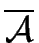 for which
for which
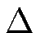 (a,
(a,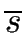 )
is known for every
a
)
is known for every
a 
 .
.
- the functions first, rest and cons
operate on lists and are similar to the
traditional stack routines top, pop and push
respectively.
Figure 6 shows a DFA
obtained from a NFA by applying Algorithm 1.
Figure 6:
Another DFA accepting the same language as the previous NFA.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.5]{DFAandNFA-2.eps}
\end{figure}](img29.png) |
Remark 1
States are generally denoted with numbers.
So if the states of the input NFA are called
1, 2, 3,...
then the states of the output DFA could be
{1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3},
{1, 2, 3}, ....
To simplify notation we denote the subset
{i, j,...},
by ij ... providing that there is no ambiguity.


Next: Non-deterministic Finite Automata with instantaneous
Up: Finite Automata
Previous: Deterministic Finite Automata
Marc Moreno Maza
2004-12-02
![]() = {a, b} consisting of the words
which end with b.
= {a, b} consisting of the words
which end with b.
![]() from
from ![]() one proceeds as follows.
one proceeds as follows.