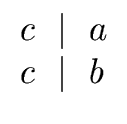  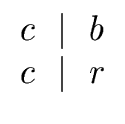 |
(7) |
where x | z means that x divides z, that is there exists y such that xy = z.
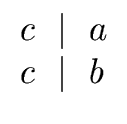  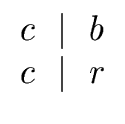 |
(7) |
Let k be the greatest value of i in Algorithm 1 such that ri
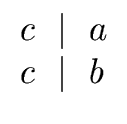  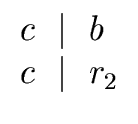  ... ...  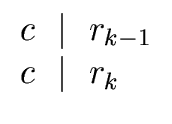  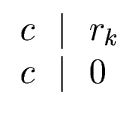 |
(8) |
(37) -> a:= (4*x-1/2) * (x+2) * (5*x+1) * (1/20*x+1)
4 883 3 333 2 49
(37) x + --- x + --- x + -- x - 1
40 8 20
(38) -> b := (4*x-1/2) * (x+4) * (5*x-1) * (1/20*x+1)
4 947 3 2889 2 127
(38) x + --- x + ---- x - --- x + 2
40 40 5
(39) -> r2 := a rem b
8 3 153 2 557
(39) - - x - --- x + --- x - 3
5 5 20
(40) -> r3 := b rem r2
209 2 33231 209
(40) --- x + ----- x - ---
80 640 32
(41) -> r4 := r2 rem r3
(41) 0
euclideanGcd(a,b) ==
a:=unitCanonical a
b:=unitCanonical b
while not zero? b repeat
(a,b):= (b,a rem b)
b:=unitCanonical b
return a
where unitCanonical: %
(2) -> a: P := (4*x-1/2) * (x+2) * (5*x+1) * (1/20*x+1)
4 883 3 333 2 49
(2) x + --- x + --- x + -- x - 1
40 8 20
(3) -> b: P := (4*x-1/2) * (x+4) * (5*x-1) * (1/20*x+1)
4 947 3 2889 2 127
(3) x + --- x + ---- x - --- x + 2
40 40 5
(4) -> r2 := unitCanonical(a rem b)
3 153 2 557 15
(4) x + --- x - --- x + --
8 32 8
(5) -> r3 := unitCanonical(b rem r2)
2 159 5
(5) x + --- x - -
8 2
(6) -> r4 := unitCanonical(r2 rem r3)
(6) 0