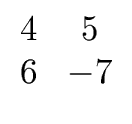

Next: Bibliography
Up: Modular Algorithms and interpolation
Previous: The Chinese Remaindering Algorithm
Consider a square matrix A of order n with coefficients in
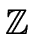 .
It is known that det(A), the determinant of A, can be computed
in at most 2n3 operations in
.
It is known that det(A), the determinant of A, can be computed
in at most 2n3 operations in
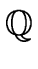 by means of Gaussian elimination.
Let us estimate the growth of the coefficients.
For simplicity, assume
by means of Gaussian elimination.
Let us estimate the growth of the coefficients.
For simplicity, assume
- A is not singular,
- no row or column permutations are necessary,
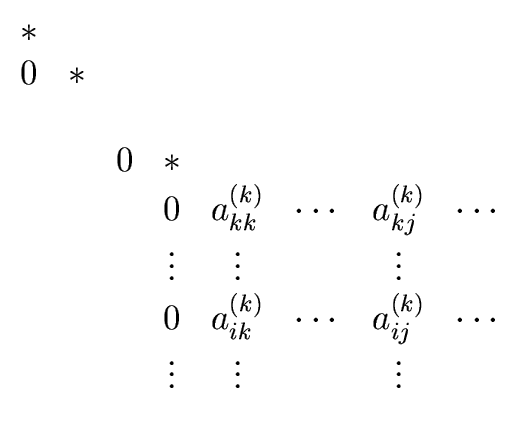
After k - 1 pivoting stages the current matrxi A(k) looks like
The entries of the matrix for
k < i 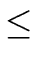 n and
k
n and
k 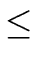 j
j 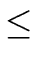 n
change according to the formula
n
change according to the formula
aij(k+1) = aij(k) - 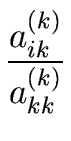 akj(k). akj(k). |
(78) |
We consider the following numbers.
- Let bk be an upper bound for the absolute value of the numerators
and the denominators of all
aij(k).
- In particular for
1
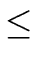 i, j
i, j 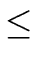 n we have
| aij |
n we have
| aij | 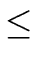 b0.
b0.
From Relation (78) we obtain
bk 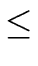 2bk-14 2bk-14 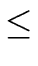 4bk-242 4bk-242 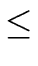 ... ... 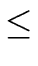 2kb04k 2kb04k |
(79) |
This shows an exponential upper bound.
(However a polynomial bound in b0, n can be established
but the proof is far from trivial and the formula still not very encouraging.)
In what follows, we present an approach whose goal is control
the growth of the intermediate computations when calculating the determinant of A.
Let d be this determinant.
Let us choose a prime number
p 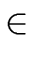
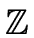 such that
such that
Let r be the determinant of A regarded as a matrix over
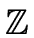 /p
/p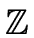 and let us choose for representing
and let us choose for representing
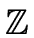 /p
/p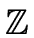 the integers in the symmetric range
the integers in the symmetric range
- 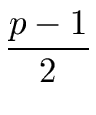 ... ... 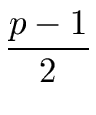 |
(81) |
Hence we have
leading to
Observe that det(A) is a polynomial in the coefficients of A.
For instance with n = 2 we have
| det(A) = a11 a22 - a12 a21 |
(84) |
which shows that det(A) (for n = 2) is a polynomial in
a11, a22, a12, a21.
Observe also the map
h : 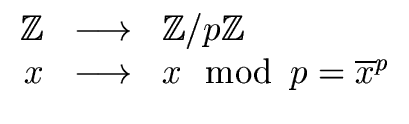 |
(85) |
is a ring homomorphism. In other words for every
x, y 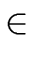
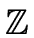 we have
we have
Hence for n = 2 we have
More generally we have
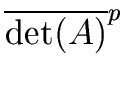 = det(A mod p) = det(A mod p) |
(88) |
that is
d 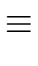 r mod p r mod p |
(89) |
which means that p divides d - r.
This with Relation (83) leads to
Hence the determinant of A as a matrix over
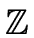 is equal to the determinant of A regarded as a matrix over
is equal to the determinant of A regarded as a matrix over
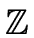 /p
/p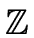 .
Therefore the computation of the determinant of A as a matrix over
.
Therefore the computation of the determinant of A as a matrix over
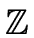 can be done modulo p, which provides a control on the intermediate computations.
Now we have to answer the following questions:
can be done modulo p, which provides a control on the intermediate computations.
Now we have to answer the following questions:
- How to choose p?
- What do we win?
For choosing p we need an a-priori bound for the determinant of A.
This is given by the following Hadamard's inequality.
Theorem 6
Let
B be the maximal absolute value of an entry of
A.
Then we have
| d | 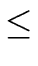 nn/2 Bn nn/2 Bn |
(91) |
Example 4
Consider
Gaussian elimination leads to
Hence
det(A) = - 58.
The Hadamard's inequality gives
| det(A) | 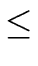 21 72 = 98 21 72 = 98 |
(94) |
The number p = 199 is prime and satisfies
p > 2×98.
Gaussian elimination
mod p leads to
So
det(A mod p) = 141 = - 58 in
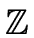 /199
/199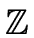 .
.
Let us study what is the cost of this approach.
Let us denote by C the determinant bound of Hadamard's inequality.
Assume that our machine words are N-bit long.
We make the following observations.
Therefore we have proved the following theorem
Theorem 7
The determinant of a square matrix with order
n, coefficients in
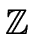
and
B as the maximal absolute value of a coefficient can be computed in
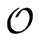
(
n3 n2 (log
n + log
B)
2) word operations.
This is not in fact a big progress w.r.t. Gaussian elimination over
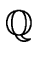 .
But this can be improved using a small primes modular computation
as follows.
.
But this can be improved using a small primes modular computation
as follows.
Algorithm 5
![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $A=(a_{ij...
...\
\> \> $d$\ := $d - m$\ \\
\> {\bf return}($d$)
\end{tabbing}\end{minipage}}](img137.png)
Proof.
Recall that det(
A) is a polynomial expression in the coefficients of
A.
Hence by using the ring homomorphism between
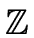
and
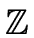
/
mi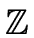
for
i = 0
... r - 1 we have
det(A) 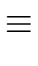 dimod mi dimod mi |
(97) |
Using the ring isomorphism of Corollary
2
we deduce
det(A) 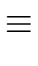 d mod m d mod m |
(99) |
where
m is the product of the moduli
m0,...,
mr-1.
Now observe that
| m |
= |
m0 ... mr-1 |
| |
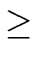 |
2r |
| |
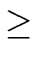 |
2 C + 1 |
| |
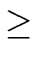 |
2 nn/2 Bn |
| |
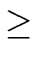 |
2 | d | |
|
(100) |
Hence actually we have
det(
A) =
d.

Example 5
Consider again
We choose the four primes 2, 3, 5, 7 so that m = 210.
We get
det(A) 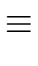 0 mod 2 0 mod 2 |
|
det(A) 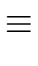 2 mod 3 2 mod 3 |
det(A) 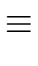 2 mod 5 2 mod 5 |
|
det(A) 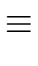 - 2 mod 7 - 2 mod 7 |
|
(102) |
The solutions of the system
d  dimod mi
for
1
dimod mi
for
1 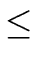 i
i 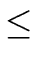 4 are in
4 are in
-58 + 210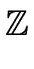 = {..., - 268, - 58, 152, 362,...} = {..., - 268, - 58, 152, 362,...} |
(103) |
Finally
det(A) = - 58 again.
Based on this small primes modular computation approach
one could prove the following theorem
Theorem 8
The determinant of a square matrix with order
n, coefficients in
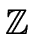
and
B as the maximal absolute value of a coefficient can be computed in
(
n4log
2(
n B)(log
2n + log
2B)) word operations.
Proof.
See Theorem 5.12 in [
vzGG99]

Remark 10
With Algorithm 5
we achieve the following goals.
- All intermediate computations can be made modulo small prime numbers.
In practice these small primes are machine integers
allowing fast computations.
- The only possible large value is the determinant itself.
- The space and the time required for the whole computation can be estimated
in advance.
Moreover the computations of the modular determinants (the di's)
are pairwise independent and thus can be distributed.


Next: Bibliography
Up: Modular Algorithms and interpolation
Previous: The Chinese Remaindering Algorithm
Marc Moreno Maza
2003-06-06

![]()
![]() such that
such that
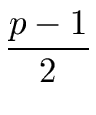 ...
... 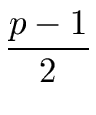
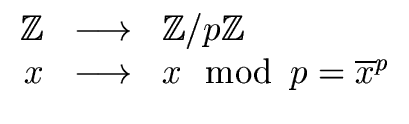
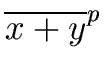 =
= 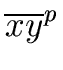 =
= 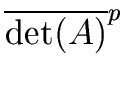 =
= 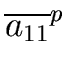
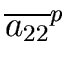 -
- 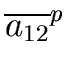
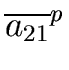
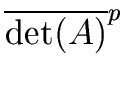 = det(A mod p)
= det(A mod p)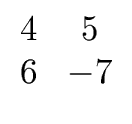
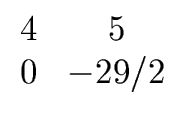
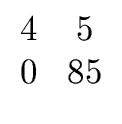
![]() .
But this can be improved using a small primes modular computation
as follows.
.
But this can be improved using a small primes modular computation
as follows.