Theorem 11
Let
R be a commutative ring with unity.
Let
a and
b be univariate polynomials over
R
with respective degrees
n and
m such that
n 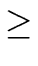 m
m 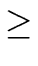
0 and
b 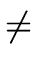
0 monic.
Algorithm
7
computes the quotient and the remainder of
a w.r.t.
b
in
4
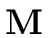
(
n -
m) +
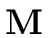
(
m) +
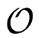
(
m)
operations in
R Proof.
We do not give here a proof and we refer to Theorem 9.5 in [
vzGG99].
However, roughly speaking, Algorithm
7
consists essentially in
- c multiplications (where c is a constant) to compute g (by virtue of
Theorem 9),
- one multiplication to compute q,
- one multiplication to compute r.

![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $a,b \in ...
...\> $r$\ := $a - b \, q$\ \\
\> {\bf return} $(q,r)$\end{tabbing}\end{minipage}}](img150.png)