

Next: Solving polynomial equations via Newton
Up: Advanced Computer Algebra: From Newton
Previous: Division with remainder using Newton
Let R be a commutative ring with unity.
Let f, g, h be univariate polynomials in R[x]
and let m 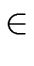 R.
We assume that the following relation holds
R.
We assume that the following relation holds
f  g h modm g h modm |
(83) |
We aim to lift this factorization modulo m into a factorization modulo m2.
Hence we want to compute
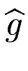 and
and
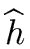 such that
such that
We will refer to this problem as the factorization lifting problem.
To do so we will assume that we are given two polynomials
s and t such that
sg + th  1 modm 1 modm |
(85) |
Hence we will say that g and h are coprime modulo m.
When R/m is a field then we can compute s and t
by applying the Extended Euclidean Algorithm in R[x]/m.
Proposition 8
A solution to the factorization lifting problem
of Equation
84
is given by
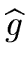 = g + t e and = g + t e and 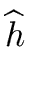 = h + s e where e = f - g h = h + s e where e = f - g h |
(86) |
Proof.
We have the following relations.
f - 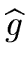 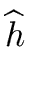 |
= |
f - (g + t e) (h + s e) |
|
| |
= |
f - g h - g s e - h t e - s t e2 |
|
| |
= |
e - (s g + t h) e - s t e2 |
|
| |
= |
(1 - s g + t h) e - s t e2 |
|
| |
 |
(1 - s g + t h) e - s t e2 |
modm2 |
|
(87) |
By hypothesis
e  0 modm and (1 - s g + t h) 0 modm and (1 - s g + t h)  0 modm 0 modm |
(88) |
Hence both
(1 -
s g +
t h)
e and
e2 are mutiple of
m2.
It follows that

Remark 16
Observe that Proposition 8
works also if f, g, h are constants of R.
In other words, f, g, h do not need to be polynomials!
The factorization lifting problem and its solution
by Proposition 8
are valid in any commutative ring with unity.
But for this solution to be an algorithm
one needs to be able to compute the Bézout coefficients s and t.
Example 7
Consider
f = x4 - 1, g = x - 2,
h = x3 + 2 x2 - x - 2
and m = 5.
We have the following computation in AXIOM
N := NonNegativeInteger
(1) NonNegativeInteger
Type: Domain
Z := Integer
(2) Integer
Type: Domain
U := UnivariatePolynomial(x,Z)
(3) UnivariatePolynomial(x,Integer)
Type: Domain
m: Z := 5
(4) 5
Type: Integer
f: U := x^4 - 1
4
(5) x - 1
Type: UnivariatePolynomial(x,Integer)
g: U := x - 2
(6) x - 2
Type: UnivariatePolynomial(x,Integer)
h: U := x^3 + 2 *x^2 -x -2
3 2
(7) x + 2x - x - 2
Type: UnivariatePolynomial(x,Integer)
e := f - g*h
2
(8) 5x - 5
Type: UnivariatePolynomial(x,Integer)
K5 := PrimeField(5)
(9) PrimeField
Type: Domain
U5 := UnivariatePolynomial(x,K5)
(10) UnivariatePolynomial(x,PrimeField 5)
Type: Domain
f5: U5 := f :: U5
4
(11) x + 4
Type: UnivariatePolynomial(x,PrimeField 5)
g5: U5 := g :: U5
(12) x + 3
Type: UnivariatePolynomial(x,PrimeField 5)
h5: U5 := h ::U5
3 2
(13) x + 2x + 4x + 3
Type: UnivariatePolynomial(x,PrimeField 5)
res := extendedEuclidean(g5,h5)
2
(14) [coef1= 2x + 3x + 4,coef2= 3,generator= 1]
s5: U5 := res.coef1
2
(15) 2x + 3x + 4
Type: UnivariatePolynomial(x,PrimeField 5)
t5: U5 := res.coef2
(16) 3
Type: UnivariatePolynomial(x,PrimeField 5)
g_^ := g + t5 :: U * e
2
(17) 15x + x - 17
Type: UnivariatePolynomial(x,Integer)
h_^ := h + s5 :: U * e
4 3 2
(18) 10x + 16x + 12x - 16x - 22
Type: UnivariatePolynomial(x,Integer)
factor(f - g_^ * h_^ )
4 3 2
(19) - 25(x - 1)(x + 1)(6x + 10x + 7x - 10x - 15)
Type: Factored UnivariatePolynomial(x,Integer)
Proposition 9
Let
a and
b be in
R[
x] such that
b is monic.
Let
q and
r be the quotient and the remainder of
a w.r.t.
b.
Let
m be in
R.
If
a 
0 mod
m then
q  0 modm and r 0 modm and r  0 modm 0 modm |
(91) |
also hold.
Proof.
There exists
a * 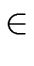 R
R[
x] such that
a =
m a * .
Let
q * and
r * be the quotient and the remainder of
a * w.r.t.
b.
Then we have
| a * = q * b + r * and deg r * < deg b |
(92) |
Hence we have
| a = m q * b + m r * and deg (m r * ) < deg b |
(93) |
Since the quotient and the remainder of
a w.r.t.
b are unique
we have
| q = m q * and r = m r * |
(94) |

Definition 6
Let
f,
g,
h,
s,
t be polynomials in
R[
x] and let
m 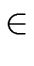 R
R.
We say that
(
f,
g,
h,
s,
t) is a
liftable quintet modulo
m
if the following conditions hold
-
f
 g h modm,
g h modm,
-
s g + t h
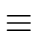 1 modm,
1 modm,
- h is monic,
-
deg f = deg g + deg h,
-
deg s < deg h,
-
deg t < deg g.
Algorithm 8
![\fbox{
\begin{minipage}{12 cm}
\begin{description}
\item[{\bf Input:}] $f,g,h,s,...
...rn} $(g^{\ast}, h^{\ast}, s^{\ast}, t^{\ast})$\ \\
\end{tabbing}\end{minipage}}](img155.png)
Theorem 12
Algorithm
8 works correctly.
Let
n = deg
f.
If
R =
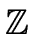
and all input polynomials have max-norm less than
m2
then it requires
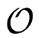
(
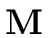
(
n)
(log
m)) word operations.
Proof.
We shall prove the following claims about
g * and
h * :
-
f - g * h *
 0 modm2,
0 modm2,
-
g *
 g modm,
g modm,
-
h *
 h modm,
h modm,
- h * monic and of the same degree as h,
- g * of the same degree as g.
We calculate modulo
m2:
| f - g * h * |
 |
f - (g + te + qg)(h + se - qh) |
| |
= |
f - gh - gse + gqh - teh - tese + teqh - qgh - qgse + qgqh |
| |
= |
f - gh - gse - teh - tese + teqh - qgse + qgqh |
| |
= |
e - (sg + th)e - ste2 + qe(th + sg) + ghq2 |
| |
= |
(1 - sg - th)(f - gh) - ste2 + qe(th + sg) + ghq2 |
|
(95) |
By assumption we have
-
1 - sg - th
 0 modm
0 modm
-
f - gh
 0 modm
0 modm
Moreover
e  0 modm and se 0 modm and se  qh + r modm2 qh + r modm2 |
(96) |
by Proposition
9
imply
q  0 modm 0 modm |
(97) |
This leads to
f - g * h *  0 modm2. 0 modm2. |
(98) |
Now the relation defining
g *
| g * = (q + t e + q g) modm2 |
(99) |
together with
e 
0 mod
m and
q 
0 mod
m
imply
g *  g modm g modm |
(100) |
Similarly we have
h *  h modm h modm |
(101) |
Now observe that by definition of
r we have
Then since
| h * = (h + r) modm2 |
(103) |
we obtain
| h monic and deg h = deg h * |
(104) |
These last relations together with
f  g * h * modm2 g * h * modm2 |
(105) |
imply
| deg g * |
= |
deg f - deg h * |
| |
= |
deg f - deg h |
| |
= |
deg g |
|
(106) |
This concludes this proof.
We refer to Theorem 15.11 in [
vzGG99] for the other claims
of the theorem.

Example 8
Consider
f = x4 - 1, g = x - 2,
h = x3 + 2 x2 - x - 2
and m = 5.
Using Proposition 8
we computed
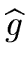 = 15x2 + x - 17 and = 15x2 + x - 17 and 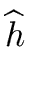 = 10x4 + 16x3 + 12x2 - 16x - 22 = 10x4 + 16x3 + 12x2 - 16x - 22 |
(107) |
Now using the improved formula of
Algorithm 8 we have the following AXIOM session
N := NonNegativeInteger
(1) NonNegativeInteger
Type: Domain
Z := Integer
(2) Integer
Type: Domain
U := UnivariatePolynomial(x,Z)
(3) UnivariatePolynomial(x,Integer)
Type: Domain
m: Z := 5
(4) 5
Type: Integer
f: U := x^4 - 1
4
(5) x - 1
Type: UnivariatePolynomial(x,Integer)
g: U := x - 2
(6) x - 2
Type: UnivariatePolynomial(x,Integer)
h: U := x^3 + 2 *x^2 -x -2
3 2
(7) x + 2x - x - 2
Type: UnivariatePolynomial(x,Integer)
e := f - g*h
2
(8) 5x - 5
Type: UnivariatePolynomial(x,Integer)
K5 := PrimeField(5)
(9) PrimeField 5
Type: Domain
U5 := UnivariatePolynomial(x,K5)
(10) UnivariatePolynomial(x,PrimeField 5)
Type: Domain
f5: U5 := f :: U5
4
(11) x + 4
Type: UnivariatePolynomial(x,PrimeField 5)
g5: U5 := g :: U5
(12) x + 3
Type: UnivariatePolynomial(x,PrimeField 5)
h5: U5 := h ::U5
3 2
(13) x + 2x + 4x + 3
Type: UnivariatePolynomial(x,PrimeField 5)
res := extendedEuclidean(g5,h5)
2
(14) [coef1= 2x + 3x + 4,coef2= 3,generator= 1]
Type: Record(coef1: UnivariatePolynomial(x,PrimeField 5),
coef2: UnivariatePolynomial(x,PrimeField 5),
generator: UnivariatePolynomial(x,PrimeField 5))
s5: U5 := res.coef1
2
(15) 2x + 3x + 4
Type: UnivariatePolynomial(x,PrimeField 5)
s: U := s5 :: U
2
(16) 2x + 3x + 4
Type: UnivariatePolynomial(x,Integer)
t5: U5 := res.coef2
(17) 3
Type: UnivariatePolynomial(x,PrimeField 5)
t: U := t5 :: U
(18) 3
Type: UnivariatePolynomial(x,Integer)
R25 := IntegerMod(25)
(19) IntegerMod 25
Type: Domain
U25 := UnivariatePolynomial(x,R25)
(20) UnivariatePolynomial(x,IntegerMod 25)
Type: Domain
e25 := f::U25 - g::U25 * h::U25
2
(21) 5x + 20
Type: UnivariatePolynomial(x,IntegerMod 25)
e : U := e25 :: U
2
(22) 5x + 20
Type: UnivariatePolynomial(x,Integer)
res := monicDivide(s*e, h)
2
(23) [quotient= 10x - 5,remainder= 80x + 75x + 70]
Type: Record(quotient: UnivariatePolynomial(x,Integer),
remainder: UnivariatePolynomial(x,Integer))
q25: U25 := res.quotient :: U25
(24) 10x + 20
Type: UnivariatePolynomial(x,IntegerMod 25)
r25: U25 := res.remainder :: U25
2
(25) 5x + 20
Type: UnivariatePolynomial(x,IntegerMod 25)
g_* := (g::U25 + t::U25 * e25 + q25 * (g::U25)) :: U
(26) x + 18
Type: UnivariatePolynomial(x,Integer)
h_* := (h::U25 + r25) :: U
3 2
(27) x + 7x + 24x + 18
Type: UnivariatePolynomial(x,Integer)
(f - g_* * h_*) :: U25
(28) 0
Type: UnivariatePolynomial(x,IntegerMod 25)
Theorem 13
Let
R be a commutative ring with unity, an element
m 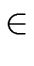 R
R
which is not a zero divisor, an integer
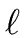
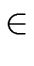

and nonzero univariate polynomials
g,
h,
g * ,
h * ,
s,
t 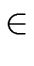 R
R[
x]
such that
-
sg + th
 1 modm
1 modm
- the leading coefficients of g and h are not zero divisors modulo m
- the polynomials g and g * have the same leading coefficients,
the same degree and coincide modulo m
- the polynomials h and h * have the same leading coefficients,
the same degree and coincide modulo m
-
gh
 g * h * modm
g * h * modm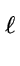
Then we have
g  g * modm g * modm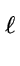 and h and h  h * modm h * modm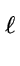 |
(108) |
Proof.
We assume to the contrary that
g 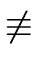 g * modm g * modm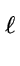 or h or h 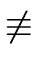 h * modm h * modm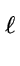 |
(109) |
Let
1
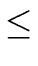 i
i <
be maximal such that
mi both divides
g * -
g and
h * -
h.
Thus there exist polynomials
u,
v  R
R[
x] such that
| g * - g = u mi and h * - h = v mi |
(110) |
and also
m does not divide
u or
v.
We may assume that
m does not divide
u.
Now we have
| 0 |
 |
g * h * - gh modm |
| |
= |
g * (h * - h) + h(g * - g) |
| |
= |
g * v mi + hu mi |
|
(111) |
This means that
m
divides
g * v mi +
hu mi.
In other words there exist
w 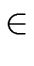 R
R[
x] such that
(g * v + hu)mi = m w w |
(112) |
Since
m is not a zero divisor in
R we have
(g * v + hu) = m -i w -i w |
(113) |
which implies
g * v + hu  0 modm 0 modm |
(114) |
Recall also that we have
th  1 - sg modm 1 - sg modm |
(115) |
and
g *  g modm and h * g modm and h *  h modm h modm |
(116) |
Therefore we obtain the following calculation modulo
m
| 0 |
 |
t(g * v + hu) |
| |
 |
tg * v + thu |
| |
 |
tg * v + (1 - sg)u |
| |
 |
(tv - su)g + u |
|
(117) |
This shows that
g divides
u modulo
m.
However from
g * -
g =
u mi
together with the facts that
g * and
g have same
leading coefficient and degree shows that
Since the leading of coefficient of
g is not a zero divisor
modulo
m we must have
u  0 modm 0 modm |
(119) |
A contradiction.
Therefore the theorem is proved.



Next: Solving polynomial equations via Newton
Up: Advanced Computer Algebra: From Newton
Previous: Division with remainder using Newton
Marc Moreno Maza
2003-06-06