Let n be a positive integer and
![]()
![]() R be a primitive n-th
root of unity.
R be a primitive n-th
root of unity.
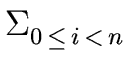 fi xi and
g =
fi xi and
g = 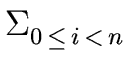 gi xi
in R[x] is the polynomial
gi xi
in R[x] is the polynomial
h = 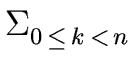 hk xk hk xk |
(17) |
hk = 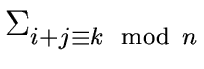 fi gj fi gj |
(18) |
p = 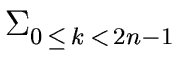 pk xk pk xk |
(19) |
pk = 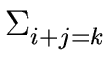 fi gj fi gj |
(20) |
|
(21) |
| f * g |
(22) |
| f = x3 + 1 and g = 2x3 + 3x2 + x + 1. | (23) |
|
(24) |
| f * g = 3x3 + 4x + 2 | (25) |
| DFT |
(26) |
| f * g = f g + q (xn - 1) | (27) |
|
(28) |
E![$\displaystyle \begin{array}{rcl} R[x] & \longmapsto & R^n \\ f & \longmapsto & (f(1), f({\omega}), f({\omega}^2), \ldots, f({\omega}^{n-1})) \end{array}$](img69.png) |
(29) |
| R[x]/ |
(30) |
If R is a field, then this a special case of the Chinese Remaindering Theorem
where
mi = x - ![]() for
i = 0 ... n - 1.
for
i = 0 ... n - 1.