

Next: Fast Convolution and Multiplication
Up: Fast Polynomial Multiplication based on
Previous: Convolution of polynomials
The Fast Fourier Transform computes the DFT quickly.
This important algorithm for computer science
(not only computer algebra, but also digital signal
processing for instance) was (re)-discovered
in 1965 by Cooley and Tukey.
Let n be a positive even integer,
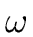
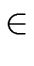 R be a primitive n-th
root of unity and
f =
R be a primitive n-th
root of unity and
f = 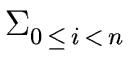 fi xi.
In order to evaluate f at
1,
fi xi.
In order to evaluate f at
1,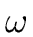 ,
,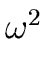 ,...,
,...,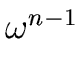 .
we divide f by
xn/2 - 1 and
xn/2 + 1 with remainder.
So let
q0, q1, r0, r1 be polynomials such that
.
we divide f by
xn/2 - 1 and
xn/2 + 1 with remainder.
So let
q0, q1, r0, r1 be polynomials such that
f = q0(xn/2 - 1) + r0 with 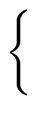 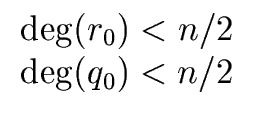 |
(31) |
and
f = q1(xn/2 + 1) + r1 with  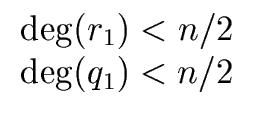 |
(32) |
The relations
deg(q0) < n/2 and
deg(q1) < n/2
hold because the polynomial f has degree less than n.
Observe that the computation of
(q0, r0) and
(q1, r1)
can be done very easily.
Indeed, let
F0, F1  R[x] be such that
R[x] be such that
f = F1 xn/2 + F0 with 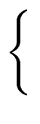 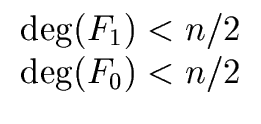 |
(33) |
We have
| f = F1(xn/2 - 1) + F0 + F1 and f = F1(xn/2 + 1) + F0 - F1 |
(34) |
Hence we obtain
| r0 = F0 + F1 and r1 = F0 - F1 |
(35) |
Let i be an integer such that
0 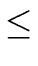 i < n/2.
By using Relation (31) with
x =
i < n/2.
By using Relation (31) with
x = 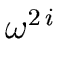 we obtain
we obtain
f (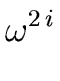 ) = q0( ) = q0(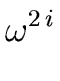 )( )(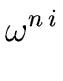 - 1) + r0( - 1) + r0(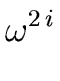 ) = r0( ) = r0(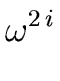 ) ) |
(36) |
since
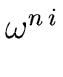 = 1.
Then, by using Relation (32) with
x =
= 1.
Then, by using Relation (32) with
x = 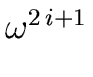 we obtain
we obtain
f (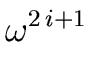 ) = q1( ) = q1(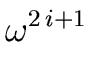 )( )(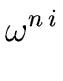 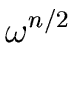 + 1) + r1( + 1) + r1(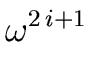 ) = r1( ) = r1(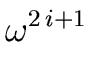 ) ) |
(37) |
since
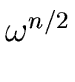 = - 1.
Indeed, this last equation follows from
= - 1.
Indeed, this last equation follows from
0 =  - 1 = ( - 1 = (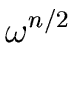 - 1)( - 1)(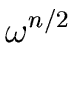 + 1) + 1) |
(38) |
and the fact that
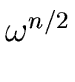 - 1 is not zero
nor a zero divisor.
Therefore we have proved the following
- 1 is not zero
nor a zero divisor.
Therefore we have proved the following
Proposition 4
Evaluating
f 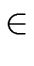 R
R[
x] (with degree less than
n)
at
1,
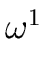
,...,
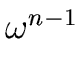
is equivalent to
- evaluate r0 at the even powers
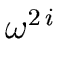 for
0
for
0 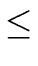 i < n/2.
i < n/2.
- evaluate r1 at the odd powers
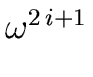 for
0
for
0 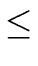 i < n/2.
i < n/2.
Since it is easy to show that
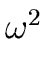 is a primitive n/2-th root of unity
we can hope for a recursive algorithm.
This algorithm would be easier if both r0 and r1 would
be evaluated at the same points.
So we define
is a primitive n/2-th root of unity
we can hope for a recursive algorithm.
This algorithm would be easier if both r0 and r1 would
be evaluated at the same points.
So we define
r1(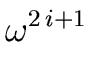 ) = r1 * ( ) = r1 * (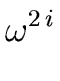 ) ) |
(39) |
Now we obtain the following algorithm.
Algorithm 1
![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $n = 2^k$...
...({\omega}^{n-2}), r_1^{\ast}({\omega}^{n-2}))$\ \\
\end{tabbing}\end{minipage}}](img89.png)
Theorem 1
Let
n be a power of 2 and
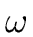
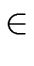 R
R a primitive
n-th
root of unity.
Then Algorithm
1 computes
DTF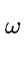
(
f ) using
-
n log(n) additions in R,
-
(n/2) log(n) multiplications by powers of
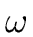 .
.
leading in total to
3/2
n log(
n) ring operations.
Proof.
By induction on
k = log
2(
n).
Let
S(
n) and
T(
n) be the number of additions
and multiplications in
R that the algorithms requires
for an input of size
n.
If
k = 0 the algorithm returns (
f0) whose costs is null
thus we have
S(0) = 0 and
T(0) = 0 which satisfies
the formula since
log(
n) = log(1) = 0.
Assume
k > 0.
Just by looking at the algorithm we that
| S(n) = 2 S(n/2) + n and T(n) = 2 T(n/2) + n/2 |
(40) |
leading to the result by plugging in the induction hypothesis.



Next: Fast Convolution and Multiplication
Up: Fast Polynomial Multiplication based on
Previous: Convolution of polynomials
Marc Moreno Maza
2003-06-06
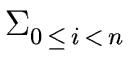 fi xi.
In order to evaluate f at
1,
fi xi.
In order to evaluate f at
1,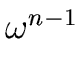 .
we divide f by
xn/2 - 1 and
xn/2 + 1 with remainder.
So let
q0, q1, r0, r1 be polynomials such that
.
we divide f by
xn/2 - 1 and
xn/2 + 1 with remainder.
So let
q0, q1, r0, r1 be polynomials such that
![]()
![]() R be a primitive n-th
root of unity and
f =
R be a primitive n-th
root of unity and
f = 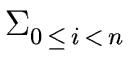 fi xi.
In order to evaluate f at
1,
fi xi.
In order to evaluate f at
1,![]() ,
,![]() ,...,
,...,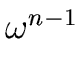 .
we divide f by
xn/2 - 1 and
xn/2 + 1 with remainder.
So let
q0, q1, r0, r1 be polynomials such that
.
we divide f by
xn/2 - 1 and
xn/2 + 1 with remainder.
So let
q0, q1, r0, r1 be polynomials such that
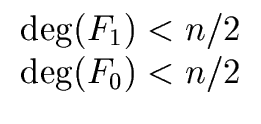
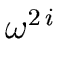 we obtain
we obtain
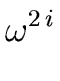 ) = q0(
) = q0(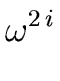 )(
)(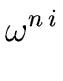 - 1) + r0(
- 1) + r0(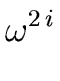 ) = r0(
) = r0(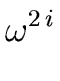 )
)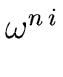 = 1.
Then, by using Relation (32) with
x =
= 1.
Then, by using Relation (32) with
x = 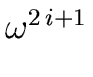 we obtain
we obtain
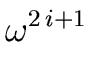 ) = q1(
) = q1(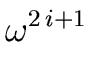 )(
)(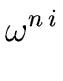
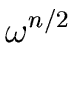 + 1) + r1(
+ 1) + r1(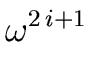 ) = r1(
) = r1(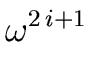 )
)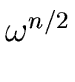 = - 1.
Indeed, this last equation follows from
= - 1.
Indeed, this last equation follows from
 - 1 = (
- 1 = (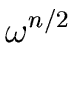 - 1)(
- 1)(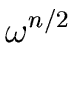 + 1)
+ 1)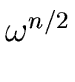 - 1 is not zero
nor a zero divisor.
Therefore we have proved the following
- 1 is not zero
nor a zero divisor.
Therefore we have proved the following
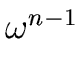 is equivalent to
is equivalent to
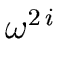 for
0
for
0 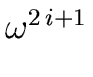 for
0
for
0 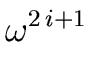 ) = r1 * (
) = r1 * (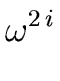 )
)