Next: The Fast Fourier Transform Up: Fast Polynomial Multiplication based on Previous: The Discrete Fourier Transform
Let ![]() be a positive integer and
be a positive integer and
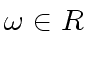 be a primitive
be a primitive ![]() -th
root of unity.
-th
root of unity.
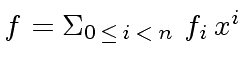 and
and
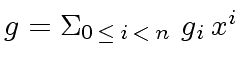 in
in ![$ R[x]$](img137.png) is the polynomial
is the polynomial
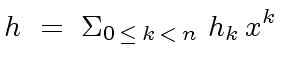 |
(17) |
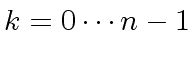 the coefficient
the coefficient 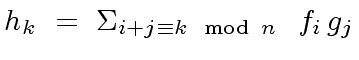 |
(18) |
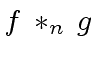 or simply by
or simply by
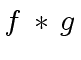 if not ambiguous.
if not ambiguous.
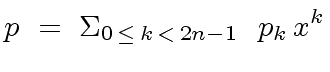 |
(19) |
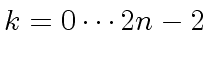 the coefficient
the coefficient 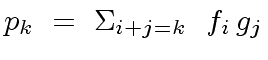 |
(20) |
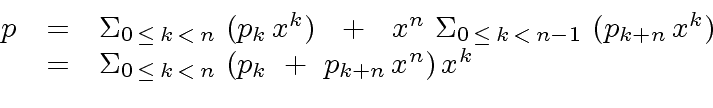 |
(21) |
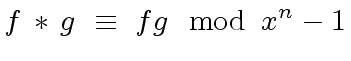 |
(22) |
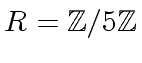 ,
, 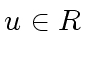 and consider the
polynomials
and consider the
polynomials
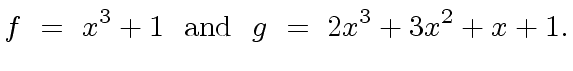 |
(23) |
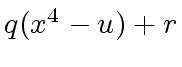 where
where 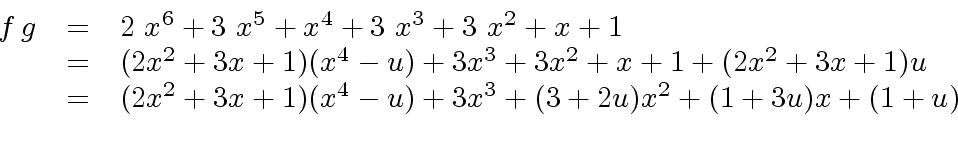 |
(24) |
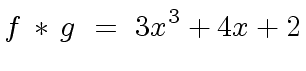 |
(25) |
![$ f,g \in R[x]$](img5.png) univariate polynomials of degree less than
univariate polynomials of degree less than 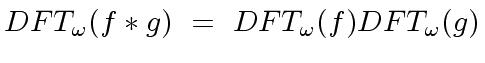 |
(26) |
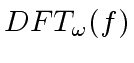 and
and
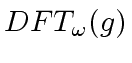 is computed componentwise.
is computed componentwise.
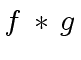 and
and 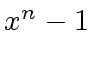 ,
there exists a polynomial
,
there exists a polynomial
![$ q \in R[x]$](img167.png) such that
such that
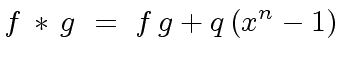 |
(27) |
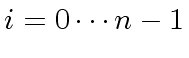 we have
we have
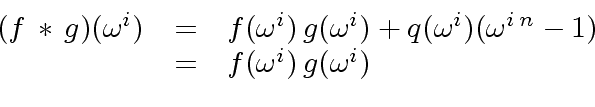 |
(28) |
![$\displaystyle E_{\omega} \, : \ \left\{ \begin{array}{rcl} R[x] & \longmapsto &...
...(1), f({\omega}), f({\omega}^2), \ldots, f({\omega}^{n-1})) \end{array} \right.$](img172.png) |
(29) |
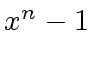 .
Since
.
Since
![$\displaystyle R[x] / \langle x^n - 1 \rangle \ \simeq \ R^n$](img174.png) |
(30) |
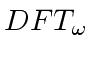 realizes this isomorphism.
realizes this isomorphism.
If ![]() is a field, then this a special case of the Chinese Remaindering Theorem
where
is a field, then this a special case of the Chinese Remaindering Theorem
where
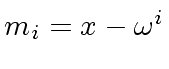 for
for
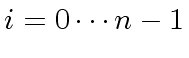 .
.
Marc Moreno Maza