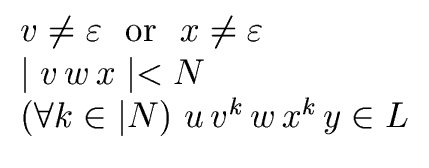

Next: Context-free grammars
Up: Grammars and Parsing
Previous: The notion of a grammar
The grammars of Example 3
have the nice following property: every production
has the form
A 
 where
A is a non-terminal symbol and
where
A is a non-terminal symbol and  is a string of grammar symbols.
These grammars are called context-free grammars
and will be studied in the next section.
They are one of the classes
of the classification of Chomsky
that we present now.
is a string of grammar symbols.
These grammars are called context-free grammars
and will be studied in the next section.
They are one of the classes
of the classification of Chomsky
that we present now.
TYPE 1. The grammar
G = (VT, VN, S, P) is of type 1
if every production has the form
Such a grammar is also called a context-sensitive grammar.
TYPE 2. The grammar
G = (VT, VN, S, P) is of type 2
if every production has the form
Such a grammar is also called a context-free grammar.
TYPE 3. The grammar
G = (VT, VN, S, P) is said right regular
if every production has the form
The grammar
G = (VT, VN, S, P) is said left regular
if every production has the form
The grammar G is said regular or of type 3
if it is either right regular or left regular.
TYPE 0. The grammar
G = (VT, VN, S, P) is of type 0
if it is not of type 1, 2 or 3.
THE TYPE OF A LANGUAGE. Let n be an integer in the range 0, 1, 2, 3.
A language L over an alphabet 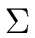 is said of type n if it is generated
by a grammar of type n and cannot be generated
by a grammar of type n + 1.
A language of type 2 is also said context-free
(or algebraic)
and a language of type 3 is also said regular.
is said of type n if it is generated
by a grammar of type n and cannot be generated
by a grammar of type n + 1.
A language of type 2 is also said context-free
(or algebraic)
and a language of type 3 is also said regular.
REGULAR LANGUAGES. Let
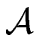 = (
= (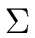 , S, s0, F,
, S, s0, F,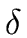 ) be a DFA.
We define the grammar
G = (
) be a DFA.
We define the grammar
G = (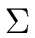 , S, s0, P) such that
, S, s0, P) such that
- its terminals are the letters of
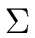 ,
,
- its non-terminals are the states of the automaton
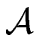 ,
,
- its start-symbol is the initial state of
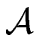 ,
,
- its productions are defined as follows: for each
x
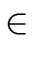
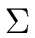 and each s
and each s 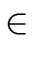 S such that
S such that
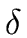 (s, x) is defined we set the rule
s
(s, x) is defined we set the rule
s  xs' where
s' =
xs' where
s' = 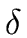 (s, x).
Moreover if s' is a final state
we set the rule
s'
(s, x).
Moreover if s' is a final state
we set the rule
s' 
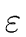 .
.
It is not hard to prove that the language recognized by 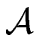 is the language generated by G.
Observe that G is a regular grammar.
Conversly, one can build a FA from a regular grammar
such that their associated languages match.
Hence we can state the following theorem.
is the language generated by G.
Observe that G is a regular grammar.
Conversly, one can build a FA from a regular grammar
such that their associated languages match.
Hence we can state the following theorem.
Theorem 1
A grammar
G is regular iff the language generated by
G
is recognized by finite automata.
CONTEXT-FREE LANGUAGES. We start with two examples of context-free languages
that we met already.
Then we give a pumping-lemma for context-free languages
as Theorem 2.
Example 6
Consider
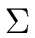 = {a, b} and
L = {anbn | n
= {a, b} and
L = {anbn | n 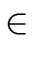
 }.
The language L is of type 2.
Indeed we already know that L is not recognized by FA and thus it is
not of type 3.
It is easy to show that L can be generated by the following context-free grammar.
}.
The language L is of type 2.
Indeed we already know that L is not recognized by FA and thus it is
not of type 3.
It is easy to show that L can be generated by the following context-free grammar.
|
S |
 |
aSb |
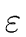 |
Theorem 2 (Bar-Hillel, Perles, Shamir)
Let
G = (
VT,
VN,
S,
P) be a context-free grammar.
There exists an integer
N such that for every word
m generated by
G with length
|
m |
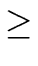 N
N
there exist words
u,
v,
w,
x,
y over
VT such that
m = u v w x y with 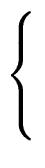 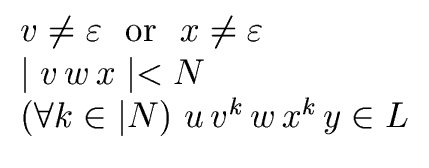 |
(13) |
Example 7
Consider the alphabet
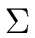 = {a, b, c} = VT
and the language
= {a, b, c} = VT
and the language
L = {anbncn | n 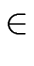 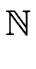 } } |
(14) |
over 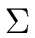 .
We define
VN = {S, T, U, W, X, Y, Z, B}.
The grammar
G = (VT, VN, S, P) with P
given by
.
We define
VN = {S, T, U, W, X, Y, Z, B}.
The grammar
G = (VT, VN, S, P) with P
given by
| S |
 |
abc |
| S |
 |
aTBc |
| TB |
 |
UB |
| UB |
 |
UW |
| UW |
 |
BW |
| BW |
 |
BT |
| Tc |
 |
XBcc |
| BX |
 |
BY |
| ZY |
 |
ZB |
| ZB |
 |
XB |
| aX |
 |
aaT |
| aX |
 |
aa |
| B |
 |
b |
| BY |
 |
ZY |
|
(15) |
generates the language L.
Theorem 2
can be used to prove that L is not a context-free language.
Therefore L is a language of type 1.


Next: Context-free grammars
Up: Grammars and Parsing
Previous: The notion of a grammar
Marc Moreno Maza
2004-12-02
![]()
![]() where
A is a non-terminal symbol and
where
A is a non-terminal symbol and ![]() is a string of grammar symbols.
These grammars are called context-free grammars
and will be studied in the next section.
They are one of the classes
of the classification of Chomsky
that we present now.
is a string of grammar symbols.
These grammars are called context-free grammars
and will be studied in the next section.
They are one of the classes
of the classification of Chomsky
that we present now.

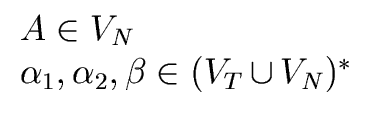

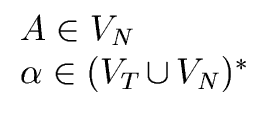
 aB or A
aB or A  a where
a where 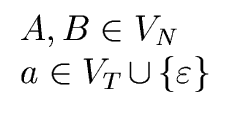
 Ba or A
Ba or A  a where
a where 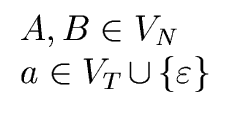
![]() is said of type n if it is generated
by a grammar of type n and cannot be generated
by a grammar of type n + 1.
A language of type 2 is also said context-free
(or algebraic)
and a language of type 3 is also said regular.
is said of type n if it is generated
by a grammar of type n and cannot be generated
by a grammar of type n + 1.
A language of type 2 is also said context-free
(or algebraic)
and a language of type 3 is also said regular.
![]() = (
= (![]() , S, s0, F,
, S, s0, F,![]() ) be a DFA.
We define the grammar
G = (
) be a DFA.
We define the grammar
G = (![]() , S, s0, P) such that
, S, s0, P) such that