3.3. Matrices#

Matrices are very useful objects with many applications. Loosely speaking, they are a two-dimensional array of or table of other mathematical objects.

\[\begin{split} \begin{bmatrix} 2 & 5 & 8 \\ -4 & 12 & 6 \\ 6 & 11 & 9 \\ \end{bmatrix} \end{split}\]

Matrices are useful both as objects themselves and as representations of other relationships or properties. As we will explore, matrices can be used to encode binary relations, functions, and even ore abstract mathematical objects like graphs (see Section 7).

3.3.1. Definitions#

A matrix is some table of numbers, symbols, or mathematical objects coming from a set. A matrix has a “height” and a “width” corresponding to the number of rows and the number of columns, respectively. We describe a matrix first by its number of rows and then by its number of columns. A “two by three matrix of integers”, shown below, has two rows, three columns, and its entries are integers.

\[\begin{split} \begin{bmatrix} 3 & 5 & 12 \\ -1 & -7 & 4 \end{bmatrix} \end{split}\]

For a particular \((i,j)\) index, we can say the \((i,j)\)th entry of a matrix is the element of the matrix in the \(i\)th row and the \(j\)th column. In the previous matrix, \(5\) is the \((1,2)\) entry. \(-7\) is the \((2,1)\) entry. Generally, we can have an \(m\) by \(n\) matrix with \(m\) rows and \(n\) columns. An \(m\) by \(n\) matrix can be denoted as \(A_{m\times n}\)

Definition (matrix)

An \(m\) by \(n\) matrix is a rectangular array of entries coming from some set organized into \(m\) rows and \(n\) columns.

We give special names to matrices with certain dimensions.

  1. When \(m = 1\) we have a row vector. Below is a row vector with \(7\) entries.

\[ \begin{bmatrix} 4 & 1 & 4 & 2 & 3 & 7 & 8 \end{bmatrix} \]

  1. When \(n = 1\) we have a column vector. Below is a column vector with \(6\) entries.

\[\begin{split} \begin{bmatrix} 5 \\ -3 \\ 4 \\ -11 \\ 22 \\ 6 \end{bmatrix} \end{split}\]

  1. When \(m=n\), we have a square matrix. We say a square matrix is of order \(n\) for a matrix with dimension \(n\) by \(n\). A square matrix of order \(3\) is shown below.

\[\begin{split} \begin{bmatrix} 9 & -1 & 16 \\ 3 & -5 & 12 \\ 11 & 4 & -8 \end{bmatrix} \end{split}\]

We can denote a \(m\) by \(n\) matrix \(A\) as \(A = (a_{i,j})\). This is similar to how we expressed sequences, but now with two indices. Unlike sequences, which may start with a term \(a_0\), matrices (almost) always start with \(a_{1,1}\) and end with \(a_{m,n}\). Since entries in a matrix come from some set \(S\), and it has a total of \(m \times n\) entries, we can view matrices as elements of \(S^{m \times n}\).

\[\begin{split} A = \begin{bmatrix} a_{1,1} & a_{1,2} & a_{1,3} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & a_{2,3} & \cdots & a_{2,n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m,1} & a_{m,2} & a_{m,3} & \cdots & a_{m,n} \\ \end{bmatrix} = (a_{i,j}) \in S^{m \times n}. \end{split}\]

We can consider the \(i\)th row of an \(m\) by \(n\) matrix as a sequence with \(n\) terms, an \(n\)-tuple, or as a row vector with \(n\) entries.

\[\begin{split} \begin{bmatrix} a_{i,1} & a_{i,2} & a_{i,3} & \cdots & a_{i,n} \\ \end{bmatrix} \in S^{n}. \end{split}\]

Similarly, the \(j\)th column is a column vector with \(n\) entries.

\[\begin{split} \begin{bmatrix} a_{1,j} \\ a_{2,j} \\ a_{3,j} \\ \vdots \\ a_{m,j} \\ \end{bmatrix} \in S^{m}$. \end{split}\]

When the entries of a matrix comes from a particular set of numbers, we can declare that matrix, for example, a “real matrix”, a “complex matrix”, or an “integer matrix”, to say its entries are real numbers, complex numbers, or integers, respectively.

Although we can view, for example, \(2\) by \(3\) real matrices as elements of \(\mathbb{R}^{2 \times 3}\). We must remember that matrices have a notion of “dimension” that generic elements of \(\mathbb{R}^{2\times3} = \mathbb{R}^6\) do not. Indeed, a \(2\) by \(3\) matrix is not the same as a \(3\) by \(2\) matrix, although both can be viewed as elements of \(\mathbb{R^6}\). Performing arithmetic on matrices will show this explicitly.

3.3.2. Operations on Matrices#

When matrices have entries coming from a set with supports addition and multiplication, like real numbers, integers, or even more general objects like polynomials, it is possible to combine them with a generalized form of arithmetic.

There are three basic operations: scalar multiplication, addition, and matrix multiplication. As we will see, two matrices must have so-called compatible dimensions, in order to be combined arithmetically.

Scalar Multiplication#

Scalar multiplication is a simple operation which multiplies a single number against each entry of a matrix to produce another matrix of the same dimensions.

Say \(A = (a_{i,j})\) is an \(m\) by \(n\) integer matrix. Given some other integer \(c\), \(cA\) is another \(m\) by \(n\) matrix where:

\[\begin{split}cA = (c \cdot a_{i,j}) &= c\begin{bmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m,1} & a_{m,2} & \cdots & a_{m,n} \\ \end{bmatrix} \\[1em] & = \begin{bmatrix} c\cdot a_{1,1} & c\cdot a_{1,2} & \cdots & c\cdot a_{1,n} \\ c\cdot a_{2,1} & c\cdot a_{2,2} & \cdots & c\cdot a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ c\cdot a_{m,1} & c\cdot a_{m,2} & \cdots & c\cdot a_{m,n} \\ \end{bmatrix} \end{split}\]

Scalar multiplication

\[\begin{split} A = \begin{bmatrix} 3 & 5 & 12 \\ -1 & -7 & 4 \end{bmatrix} \qquad 4A = \begin{bmatrix} 12 & 20 & 48 \\ -4 & -28 & 16 \end{bmatrix} \end{split}\]

Addition and Subtraction#

Two matrices can be added or subtracted when they have the same dimensions. For two \(m\) by \(n\) matrices, \(A = (a_{i,j})\) and \(B = (b_{i,j})\), their sum \(A + B\) is equal to \((a_{i,j} + b_{i,j})\). That is, each entry of \(A\) is added to the corresponding entry in \(B\) in the same position.

\[\begin{split} \begin{gather} \begin{bmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m,1} & a_{m,2} & \cdots & a_{m,n} \\ \end{bmatrix} + \begin{bmatrix} b_{1,1} & b_{1,2} & \cdots & b_{1,n} \\ b_{2,1} & b_{2,2} & \cdots & b_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m,1} & b_{m,2} & \cdots & b_{m,n} \\ \end{bmatrix} = \\[1em] \begin{bmatrix} a_{1,1} + b_{1,1} & a_{1,2} + b_{1,2} &\cdots & a_{1,n} + b_{1,n} \\ a_{2,1} + b_{2,1} & a_{2,2} + b_{2,2} & \cdots & a_{2,n} + b_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m,1} + b_{m,1} & a_{m,2} + b_{m,2} & \cdots & a_{m,n} + b_{m,n} \\ \end{bmatrix} \end{gather} \end{split}\]

Thanks to scalar multiplication, we can define subtraction via addition.

\[ A - B = A + (-1)B \]

To add or subtract matrices they must be of the same dimensions. Every entry in the first matrix must have a corresponding entry in the second matrix to be added to.

Matrix addition

\[\begin{split} \begin{bmatrix} 1 & -4 & 8\\ 11 & 2 & 24 \\ 12 & 4 & 1 \\ \end{bmatrix} + \begin{bmatrix} -9 & 8 & 6 \\ 0 & 15 & 2 \\ 3 & 14 & 0 \end{bmatrix} = \begin{bmatrix} -8 & 4 & 14 \\ 11 & 17 & 26 \\ 15 & 18 & 1 \end{bmatrix} \end{split}\]

Matrix Multiplication#

Matrix multiplication is much more involved than addition. First, we must consider under which conditions two matrices can be multiples.

Matrix multiplication between two matrices is only defined when the number of columns in the left-hand matrix equals the number of rows in the right-hand matrix. The result of the multiplication is another matrix whose number of rows equals the left-hand matrix’s and whose number of columns equals the right-hand matrix’s.

\[ A_{m\times n} \cdot B_{n\times p} = C_{m \times p} \]

In this notation, the “inner” dimensions must be the same, and the “outer” dimensions give the dimensions of the product. In this case, \(n = n\) are the inner dimensions, and \(m, p\) are the outer dimensions.

But how do we define the entries of the product \(C = (c_{i,j})\)? Each entry of the matrix product \(c_{i,j}\) is an inner product of the \(i\)th row of \(A\) and the \(j\)th column of \(B\).

\[\begin{split} c_{i,j} &= \begin{bmatrix} a_{i,1} & a_{i,2} & a_{i,3} & \cdots & a_{i,n} \\ \end{bmatrix} \cdot \begin{bmatrix} b_{1,j} \\ b_{2,j} \\ b_{3,j} \\ \vdots \\ b_{n,j} \\ \end{bmatrix} \\[1em] &= \left(a_{i,1}\cdot b_{1,j} + a_{i,2} \cdot b_{2,j} + \cdots + a_{i,n}\cdot b_{n,j}\right) \\[1em] &= \sum_{k=1}^n a_{i,k} \cdot b_{k,j} \end{split}\]

Therefore, the matrix multiplication \(A_{m\times n} \cdot B_{n\times p} = C_{m \times p}\) is actually \(m \times p\) individual inner products.

../_images/MatrixMult.svg

Fig. 3.20 A \(4\) by \(4\) matrix multiplication showing the inner product producing \(c_{2,2}\)#

Matrix multiplication

\[\begin{split} \begin{bmatrix} -9 & 6 \\ 0 & 2 \\ 3 & 0 \end{bmatrix}_{3\times\textcolor{green}{2}} & \times \begin{bmatrix} 1 & -4 & 5 \\ 7 & 2 & 2 \\ \end{bmatrix}_{\textcolor{green}{2}\times3} \\[1em] & = \begin{bmatrix} (-9 \cdot 1) + (6 \cdot 7) & (-9\cdot -4) + (6 \cdot 2) & (-9 \cdot 5) + (6 \cdot 2) \\ (0 \cdot 1) + (2 \cdot 7) & (0\cdot -4) + (2 \cdot 2) & (0 \cdot 5) + (2 \cdot 2) \\ (3 \cdot 1) + (0 \cdot 7) & (3\cdot -4) + (0 \cdot 2) & (3 \cdot 5) + (0 \cdot 2) \\ \end{bmatrix}_{3\times3} \\[1em] & = \begin{bmatrix} 33 & 48 & -33 \\ 14 & 4 & 4 \\ 3 & -12 & 15 \\ \end{bmatrix}_{3\times3}\end{split}\]

Matrix commutativity

\(A = \begin{bmatrix} 3 & 2 \\ 0 & -1 \end{bmatrix}\), \(B = \begin{bmatrix} 2 & -2 & 5 \\ 0 & -1 & 3 \\ \end{bmatrix} \)

Compute \(A \cdot B\), \(A \cdot A\), and \(B \cdot A\), if possible.

Matrix commutativity

\[\begin{split} A \cdot B = \begin{bmatrix} 6 & -8 & 21 \\ 0 & 1 & -3 \\ \end{bmatrix} \end{split}\]
\[\begin{split}A \cdot A = \begin{bmatrix} 9 & 4 \\ 0 & 1 \end{bmatrix} \end{split}\]
\[ B_{2,3} \cdot A_{2,2} \text{ is not possible!} \]

The previous checkpoint brings to light an interesting consequence of matrix multiplication. For non-square matrices, if \(A \cdot B\) is defined, then \(B \cdot A\) is not. For square matrices, \(A \cdot B\) and \(B \cdot A\) are both defined, but it is very unlikely that \(AB = BA\).

Tip

Matrix multiplication is not commutative. In general, \(AB \neq BA\).

The zero and identity matrices#

Of course, it is sometimes possible for \(AB =BA\). Two important examples are when one of the matrices is the zero matrix or the identity matrix.

The zero matrix is a matrix with all zero entries. The \(m\) by \(n\) zero matrix is denoted by \(0_{m,n}\).

\[\begin{split} 0_{m,n} = \left.\begin{bmatrix} 0 & 0 & \cdots & 0 \\ 0 & 0 & \cdots &0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 \\ \end{bmatrix}\ \right\} \small{m \text{ rows}} \end{split}\]

Assuming matrix multiplication is defined, the product of a zero matrix by any other matrix is the zero-matrix (of possibly different dimension).

Zero multiplication

\[\begin{split} \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 2 & 1 & 6 \\ 5 & 3 & 3 \\ \end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} \end{split}\]

For a matrix \(A = (a_{i,j})\) its main diagonalis the entries \(a_{i,j}\) for which \(i = j\). In a square matrix of order \(n\), there are \(n\) entries along the main diagonal. In a rectangular matrix, the smaller of the two dimensions determines the number of entries along the main diagonal.

\[\begin{split} \begin{bmatrix} \textcolor{green}{x} & 0 & 0 \\ 0 & \textcolor{green}{y} & 0 \\ 0 & 0 & \textcolor{green}{z} \\ \end{bmatrix} \qquad \begin{bmatrix} \textcolor{green}{x} & 0 & 0 \\ 0 & \textcolor{green}{y} & 0 \\ 0 & 0 & \textcolor{green}{z} \\ 0 & 0 & 0 \\ \end{bmatrix} \qquad \begin{bmatrix} \textcolor{green}{x} & 0 & 0 & 0 \\ 0 & \textcolor{green}{y} & 0 & 0\\ 0 & 0 & \textcolor{green}{z} & 0\\ \end{bmatrix} \end{split}\]

Note that the other entries need not be 0. For example, the three main diagonals of the matrices in the Zero multiplication example are \((0,0)\), \((2,3)\), and \((0,0,0)\). If all entries not on the main diagonal are 0, the we call that matrix a diagonal matrix.

The identity matrix is a square diagonal matrix with all entries of the main diagonal equal to \(1\). The identity matrix of order \(n\) is denoted \(I_n\).

The property of the identity matrix is that any other matrix multiplied by the identity is equal to itself. For an \(m\) by \(n\) matrix \(A\), we have:

\[ I_mA = AI_n = A. \]

If \(A\) is a square matrix of order \(n\), then we have:

\[ I_nA = AI_n = A. \]

We can also leave the order of the identity matrix implicit. For an \(m\) by \(n\) matrix \(A\), we write \(AI\) to mean \(A\) times \(I_n\). The dimensions of the other matrix dictate the order of the identity matrix.

Identity multiplication

\[\begin{split} \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} 2 & 1 & 6 \\ 5 & 3 & 3 \\ \end{bmatrix} = \begin{bmatrix} 2 & 1 & 6 \\ 5 & 3 & 3 \\ \end{bmatrix} \\[1em] \begin{bmatrix} 2 & 1 & 6 \\ 5 & 3 & 3 \\ \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} = \begin{bmatrix} 2 & 1 & 6 \\ 5 & 3 & 3 \\ \end{bmatrix} \end{split}\]

Powers of Matrices#

For square matrices, we can define the power of a matrix as a the repeated multiplication of the matrix with itself.

Let \(A\) be a square matrix of order \(n\). Then:

\[ A^0 = I_n, \qquad\qquad A^2 = AA, \qquad\qquad A^3 = AAA, \qquad\qquad\text{etc.} \]

The square of a matrix

\[\begin{split} \begin{bmatrix} 2 & 6 \\ 5 & 3 \\ \end{bmatrix}^2 &= \begin{bmatrix} 2 & 6 \\ 5 & 3 \\ \end{bmatrix} \cdot \begin{bmatrix} 2 & 6 \\ 5 & 3 \\ \end{bmatrix} \\[1em] &= \begin{bmatrix} 34 & 30 \\ 25 & 39 \\ \end{bmatrix}\end{split}\]

Matrix Transpose#

A transpose is an operation performed on a matrix which reverses its dimensions. In particular, it exchanges the rows of the matrix with its columns.

Given an \(m\) by \(n\) matrix \(A\), its transpose is denoted \(A^T\) and is an \(n\) by \(m\) matrix. \(A^T\) is defined as:

\[\begin{split} A &= (a_{i,j}) = \begin{bmatrix} a_{1,1} & \textcolor{green}{a_{1,2}} & \cdots & a_{1,n} \\ a_{2,1} & \textcolor{green}{a_{2,2}} & \cdots & a_{2,n} \\ a_{3,1} & \textcolor{green}{a_{3,2}} & \cdots & a_{3,n} \\ a_{4,1} & \textcolor{green}{a_{4,2}} & \cdots & a_{4,n} \\ \vdots & \textcolor{green}{\vdots} & \ddots & \vdots \\ a_{m,1} & \textcolor{green}{a_{m,2}} & \cdots & a_{m,n} \\ \end{bmatrix} \\[1em] A^T &= (a_{j,i}) = \begin{bmatrix} a_{1,1} & a_{2,1} & a_{3,1} & a_{4,1} & \cdots & a_{m,1} \\ \textcolor{green}{a_{1,2}} & \textcolor{green}{a_{2,2}} & \textcolor{green}{a_{3,2}} & \textcolor{green}{a_{4,2}} & \textcolor{green}{\cdots} & \textcolor{green}{a_{m,2} }\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{1,n} & a_{2,n} & a_{3,n} & a_{4,n} & \cdots & a_{m,n} \\ \end{bmatrix} \end{split}\]

Notice that the second column becomes the second row.

Since a transpose changes the dimensions, the transpose of a “tall” matrix, is a “wide” matrix. Visually, matrix transposition “flips” or “rotates” the entries of the matrix along its main diagonal. The entries on the main diagonal do not change. See the below animation.

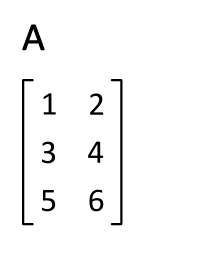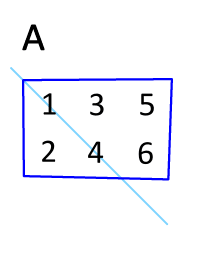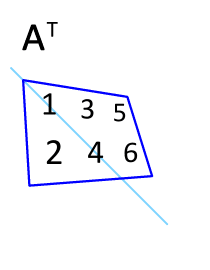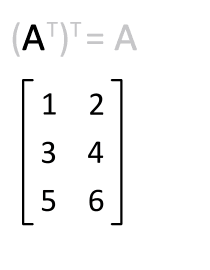
../_images/Matrix_transpose.gif

Fig. 3.21 Matrix transpose animated.#

Matrix transposition is easily reversible. Simply apply the transpose a second time.

\[ A = {(A^T)}^T \]

Notice also that the identity matrix is not affected by transposition.

\[ I = I^T = {I^T}^T \]

Matrix transpose

Compute the transpose of the below matrices.

\[\begin{split} A = \begin{bmatrix} -2 & 2 & 3 \\ 0 & 3 & 7 \\ 1 & 9 & 7 \\ \end{bmatrix} \qquad\qquad B = \begin{bmatrix} -2 & 5 & 7 \\ 12 & -11 & 8 \\ \end{bmatrix} \end{split}\]

Matrix transpose

\[\begin{split} A^T = \begin{bmatrix} -2 & 0 & 1 \\ 2 & 3 & 9 \\ 3 & 7 & 7 \\ \end{bmatrix} \qquad\qquad B^T = \begin{bmatrix} -2 & 12 \\ 5 & -11 \\ 7 & 8 \\ \end{bmatrix} \end{split}\]

3.3.3. Zero-One Matrices#

A special class of matrices whose entries come from the set \(\{0,1\}\) are called zero-one matrices. These matrices have numerous and important applications in computer science. Indeed, \(\{0,1\}\) may represent binary digits, ubiquitous in computer science.

Moreover, we can use \(\{0,1\}\) to encode truth values \(\mathbf{F}\) and \(\mathbf{T}\), respectively. This extends propositional logic to matrices. We have the following symmetries with propositional logic:

Table 3.1 Conjunction truth table for Boolean algebra#

\(a\)

\(b\)

\(a \land b\)

0

0

0

0

1

0

1

0

0

1

1

1
Table 3.2 Disjunction truth table for Boolean algebra#

\(a\)

\(b\)

\(a \lor b\)

0

0

0

0

1

1

1

0

1

1

1

1

Join and Meet#

For two zero-one matrices, we can define operations similar to matrix addition, but using \(\land\) and \(\lor\) instead of \(+\). Let \(A = (a_{i,j})\) and \(B = (b_{i,j})\) be \(m\) by \(n\) matrices.

The join of \(A\) and \(B\) is the \(m\) by \(n\) zero-one matrix defined as:

\[ A \lor B = (a_{i,j} \lor b_{i,j}) \]

The meet of \(A\) and \(B\) is the \(m\) by \(n\) zero-one matrix defined as:

\[ A \land B = (a_{i,j} \land b_{i,j}) \]

Joins and meets

\[\begin{split} A = \begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & 0 \\ \end{bmatrix} \qquad\qquad B = \begin{bmatrix} 0 & 1 & 1\\ 1 & 1 & 0\\ \end{bmatrix} \end{split}\]

The join of \(A\) and \(B\) is:

\[\begin{split} A \lor B = \begin{bmatrix} 1 \lor 0 & 0 \lor 1 & 1 \lor 1\\ 0 \lor 1& 1 \lor 1& 0 \lor 0\\ \end{bmatrix} =\ \begin{bmatrix} 1 & 1 & 1\\ 1 & 1 & 0\\ \end{bmatrix} \end{split}\]

The meet of \(A\) and \(B\) is:

\[\begin{split} A \land B = \begin{bmatrix} 1 \land 0 & 0 \land 1 & 1 \land 1\\ 0 \land 1& 1 \land 1& 0 \land 0\\ \end{bmatrix} =\ \begin{bmatrix} 0 & 0 & 1\\ 0 & 1 & 0\\ \end{bmatrix} \end{split}\]

Boolean Product#

Similar to matrix multiplication, we can define a multiplication-like operation using zero-one matrices.

The typical inner product used matrix multiplication replaced by a “disjunction of conjunctions”.

Let \(A\) be an \(m\) by \(n\) zero-one matrix and \(B\) be an \(n\) by \(p\) zero-one matrix. The boolean product of \(A\) and \(B\), denoted \(A \odot B\), is an \(m\) by \(p\) zero-one matrix with elements \(c_{i,j}\) defined as:

\[\begin{split} c_{i,j} &= \begin{bmatrix} a_{i,1} & a_{i,2} & a_{i,3} & \cdots & a_{i,n} \\ \end{bmatrix} \odot \begin{bmatrix} b_{1,j} \\ b_{2,j} \\ b_{3,j} \\ \vdots \\ b_{n,j} \\ \end{bmatrix} \\[1em] &= \left(a_{i,1}\land b_{1,j}) \ \ \lor\ \ (a_{i,2} \land b_{2,j}) \ \ \lor\ \ \cdots \ \ \lor\ \ (a_{i,n}\land b_{n,j}\right) \\[1em] \end{split}\]

Boolean product

\[\begin{split} \begin{bmatrix} 1 & 0\\ 0 & 1\\ 1 & 0\\ \end{bmatrix} &\odot \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ \end{bmatrix}\\[1em] &= \begin{bmatrix} (1 \land 1) \lor (0 \land 0) & (1\land 1) \lor (0 \land 1) & (1 \land 0) \lor (0 \land 1) \\ (0 \land 1) \lor (1 \land 0) & (0\land 1) \lor (1 \land 1) & (0 \land 0) \lor (1 \land 1) \\ (1 \land 1) \lor (0 \land 0) & (1\land 1) \lor (0 \land 1) & (1 \land 0) \lor (0 \land 1) \\ \end{bmatrix}\\[1em] &= \begin{bmatrix} 1 \lor 0 & 1 \lor 0 & 0 \lor 0 \\ 0 \lor 0 & 0 \lor 1 & 0 \lor 1 \\ 1 \lor 0 & 1 \lor 0 & 0 \lor 0 \\ \end{bmatrix}\\[1em] &= \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 1 & 0 \\ \end{bmatrix} \end{split}\]

For square zero-one matrices, we can extend Boolean product to Boolean power. Denote by \(A^{[n]}\) the Boolean product of \(A\) with itself \(n\) times. Since Boolean products are associative, the order of operations does not matter for a Boolean power.

\[ A^{[2]} = A \odot A, \qquad A^{[3]} = A^{[2]} \odot A = A \odot A^{[2]} = A \odot A \odot A, \qquad \text{etc.}\, \]

3.3.4. Relations as Matrices#

As a first application of zero-one matrices, let us recall binary relations. A binary relation \(\mathcal{R}\) from set \(A\) to set \(B\) is a subset of the Cartesian product \(A \times B\).

We previously saw that one possible view of binary relation is as a table. This table is similar to the one of the Cartesian product \(A \times B\), except that now we are only interested in some of the cells of the table. In particular, the cells corresponding to the elements of the relations.

Let \(A = \{1,2,3\}\) and \(B = \{a,b,c,d,e\}\). A binary relation from \(A\) to \(B\) could be:

\[ \{ (1,a), (1,c), (1,d), (2,a), (2,b), (3,c), (3,e) \}, \]

and its representation as a table:

\(\ \)

\(a\)

\(b\)

\(c\)

\(d\)

\(e\)

\(1\)

X

\(\ \)

X

X

\(\ \)

\(2\)

X

X

\(\ \)

\(\ \)

\(\ \)

\(3\)

\(\ \)

\(\ \)

X

\(\ \)

X

This lends itself very easily to a representation as a zero-one matrix. Since \(|A| = 3\) and \(|B| = 5\), this relation can be represented as a \(3\) by \(5\) zero-one matrix. Entries of this matrix are 1 if the corresponding tuple is in the relation, and 0 otherwise.

\[\begin{split} \begin{bmatrix} 1 & 0 & 1 & 1 & 0 \\ 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 \\ \end{bmatrix} \end{split}\]

Relational Properties and Matrices#

As a consequence of representing binary relations as matrices, we can give a visual meaning to properties to reflexive, symmetric, and antisymmetric.

A binary relation \(\mathcal{R}\) on a set \(S\) can be represented as a square zero-one matrix of order \(|S|\). Let that corresponding zero-one matrix be \(A = (a_{i,j})\).

  1. The relation is reflexive if and only if \(A\) has a 1 for every entry along its main diagonal.

  2. The relation is symmetric if and only if \(A = A^T\).

  3. The relation is antisymmetric if and only if \(a_{i,j} = 0\) or \(a_{j,i} = 0\) for \(i \neq j\).

../_images/MatrixReflexive.svg

Fig. 3.22 A reflexive relation as a matrix.#

../_images/MatrixSymmetric.svg

Fig. 3.23 A symmetric relation as a matrix.#

../_images/MatrixAntisymmetric.svg

Fig. 3.24 An antisymmetric relation as a matrix.#

An equivalent formulation for antisymmetry based on the matrix representation is:

\[ \forall i \neq j\ \ a_{i,j} = 1 \rightarrow a_{j,i} = 0. \]

A reflexive and antisymmetric matrix

Let \(\mathcal{R} = \{(1,1), (1,2), (2,2), (2, 3), (2,4), (3,3), (4,1), (4,4)\}\) be a binary relation on \(\{1,2,3,4\}\).

The zero-one matrix \(A\) represents this binary relation.

\[\begin{split} A = \begin{bmatrix} 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ \end{bmatrix} \end{split}\]

Notice that the main diagonal of \(A\) is \((1,1,1,1)\). Therefore, \(\mathcal{R}\) is reflexive. Moreover, \(\mathcal{R}\) is antisymmetric since there are no off-diagonal entries with the same value.

3.3.5. Exercises#

Exercise 3.26

Compute the matrix product.

\[\begin{split} \begin{bmatrix} 1 & 0 & 4 \\ 2 & 1 & 1 \\ 3 & 1 & 0 \\ 0 & 2 & 2 \\ \end{bmatrix} \times \begin{bmatrix} 2 & 4 \\ 1 & 1 \\ 3 & 0 \\ \end{bmatrix} \end{split}\]

Exercise 3.27

\(A = \begin{bmatrix} 1 & 2 \\ -2 & 4 \end{bmatrix}\), \(B = \begin{bmatrix} 3 & -4 & 5 \\ 2 & 1 & 0 \\ \end{bmatrix} \), \(C = \begin{bmatrix} 3 & 1 \\ 4 & 0 \\ 1 &6 \\ \end{bmatrix} \)

Are the following multiplications defined? If so, compute the product.

  1. \(A \cdot B\)

  2. \(B \cdot A\)

  3. \(C \cdot A\)

  4. \(A \cdot C\)

  5. \(B \cdot C\)

  6. \(A \cdot A\)

  7. \(B \cdot B\)

Exercise 3.28

Find all unique Boolean powers of the zero-one matrix:

\[\begin{split} A = \begin{bmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 1 & 1 & 0 \\ \end{bmatrix} \end{split}\]

Exercise 3.29

Consider the binary relation \(\mathcal{R}\) on the set \(\{1,2,3,8,9\}\) defined as

\[ \mathcal{R} = \{(a,b) \ |\ \exists n \in \mathbb{Z},\ \ a^n = b\}. \]

Give a zero-one matrix representing this relation. Is this relation reflexive? symmetric? antisymmetric? Explain why.

Exercise 3.30

Consider the binary relation \(\mathcal{R}\) on the set \(\{2,4,7,8,12\}\) defined as

\[ \mathcal{R} = \{(x,y) \ |\ \frac{y}{x} \in \mathbb{Z} \}. \]

Give a zero-one matrix representing this relation. Is this relation reflexive? symmetric? antisymmetric? Explain why.