Paths and Circuits
Contents
7.4. Paths and Circuits#
We have already seen the general idea of paths, both directed and undirected. The study of paths in graphs is a natural extension from the basic property of adjacency between two particular vertices. Rather than a single edge connecting two vertices, is there a path one can traverse between the two vertices?
This may appear to be a very simple question, but it is incredibly complex and practical. We have already seen applications of paths in the parent-child relations of trees, topological ordering of DAGs, and the strong connectivity of directed graphs.
You could conceive of many more practical applications of paths:
Determining whether a computer on the internet is reachable;
Planning a journey given specific bus/plane routes;
Optimal delivery routes for couriers; or even
Ecological interactions of organisms.
There are many special kinds of paths that have received special attention in theory and practice. In this section we review a couple of important ones.
7.4.1. Eulerian Paths and Circuits#
Given an undirected graph, can you form a simple path containing every edge? Euler tried to answer this question in the 18th century.
Definition (Euler path)
An Euler path is a path in a connected undirected graph which includes every edge exactly once.
When you have an Euler path that starts and finishes at the same vertex, you have an Euler circuit.
Definition (Euler circuit)
An Euler circuit is a circuit in a connected undirected graph which includes every edge exactly once.
Thus, every Euler circuit is an Euler path, but not every Euler path is an Euler circuit.
You can blame the people of Königsberg for the invention of graph theory (a joke). The seven bridges of Königsberg has become folklore in mathematics as the real-world problem which inspired the invention of graph theory by Euler.
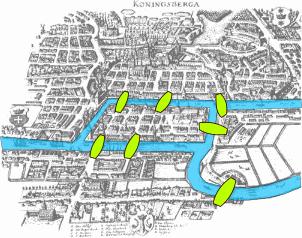
Fig. 7.65 The seven bridges of Königsberg.#
The problem is this. Can you start from somewhere in the town, travel along every bridge exactly once, and return to the same point you started?
Euler determined that the answer is no. Consider the multigraph below. It represents the connectivity of the different islands and the bridges between them.
Fig. 7.66 The seven bridges of Königsberg as a multigraph.#
We will soon see why it is impossible for this graph to have a Euler cycle. But, let’s first see some examples where it is possible.
It should be obvious that every Cycle Graph (see Cycles) admits an Euler cycle, and thus an Euler path.
Possible Euler cycles on \(C_4\) are:
\(a, b, c, d\)
\(a, d, c, b\)
\(b, c, d, a\)
\(b, a, d, c\)
\(c, d, a, b\)
\(c, b, a, d\)
\(d, a, b, c\)
\(d, c, b, a\)
Wow, so many options! But what about some more complicated examples? Sometimes just finding any Euler path is hard.
Returning to the bridges of Königsberg, how did Euler prove with certainty that there are no Euler circuits?
Fig. 7.74 The seven bridges of Königsberg as a multigraph.#
You could try every possible path… but there’s a lot. And how would you know for certain that you didn’t miss a possible path? Instead, we have a theorem that guarantees the existence of a Eulerian cycle.
Theorem 7.4.1
If a graph has an Euler circuit then every vertex must have even degree.
Proof: W.l.o.g. let the Euler circuit begin at vertex \(u\) and travel along the edge \(\{u,v\}\) to vertex \(v\). This edge contributes \(1\) to the degree of \(u\).
For each vertex traversed in the Euler circuit, the incoming edge contributes \(1\) to the vertex’s degree and the outgoing edge contributes \(1\) to the same vertex’s degree.
Finally, the circuit terminates at vertex \(u\) again, contributing \(1\) to the degree of \(u\).
Since the starting vertex \(u\) was chosen arbitrarily, it must be that an Euler circuit is only possible when every vertex in the graph has even degree. \(\blacksquare\).
A simple proof, no? Examine Fig. 7.74 again. Does every vertex have even degree? No. By contrapositive of the above theorem, since it is not the case that every vertex has even degree, then the graph cannot have an Euler circuit.
Using the same argument as in the proof of Theorem 7.4.1 we can come up with the following theorem. Its result is obvious considering that an Euler path (which is not an Euler circuit) starts and stops at different vertices. Those starting and stopping points must have odd degree.
Theorem 7.4.2
If a graph has an Euler path which is not an Euler circuit, then exactly two vertices have odd degree.
In fact, Theorem 7.4.1 can actually be more strongly stated. A graph has an Euler circuit if and only if every vertex has even degree. However, the proof of every degree vertices implying an Euler circuit is more challenging. But, it is a healthy exercise for the reader.
7.4.2. Hamilton Paths and Circuits#
What if instead of every edge in a path, what if we consider every vertex in a graph? As the title of this section suggests, we arrive at a Hamiltonian path.
Definition (Hamilton path)
A Hamilton path is a simple path in a connected undirected graph visits every vertex exactly one.
Definition (Hamilton circuit)
A Hamilton circuit is a simple circuit in a connected undirected graph which passes through every vertex other than the starting and ending vertex exactly once.
Hamilton paths and circuits are much easier to find then Euler paths and circuits. Let’s try a couple.
One Hamilton cycle of many for \(G_1\) is \(1, 4, 2, 3, 1\).
\(G_2\) does not have a Hamilton cycle, but it has several Hamilton paths. One is \(3, 4, 1, 2\).
One may feel that Euler paths and circuits are somehow “harder” than Hamilton paths and circuits. Since Euler paths must use every edge in the graph, it is more constrained than only needing every vertex. Because they are more constrained, Euler paths have nice theorems about them. Hamilton paths do not (as much).
There are no known theorems giving necessary and sufficient conditions for the existence of a Hamilton circuit. However, some sufficient conditions are known. One is Dirac’s theorem.
Theorem (Dirac’s theorem)
If a simple undirected graph has order \(n \geq 3\) and every vertex in the graph has degree greater than or equal to \(\frac{n}{2}\), then the graph has a Hamilton circuit.
Traveling Salesperson#
The classic problem for Hamilton circuits in computer science is the traveling salesperson problem. This is a classic problem in both graph theory and complexity theory. It is well-known that the traveling salesperson problem is \(NP\)-hard. That is, it cannot be solved efficiently (unless \(P = NP\)).
The traveling salesperson problem looks to find the minimal Hamilton path in a graph. What makes a Hamilton path minimal? Well, it involves a weighted graph. Something we will not study formally in this course.
But, we can give a general idea. Imagine that every edge in an undirected graph has a “weight”, “cost”, or “distance” for traveling along it. Can you find the “minimum cost” or “minimum distance” Hamilton circuit in this graph? That is the traveling salesperson problem.
Note that edge weights have nothing to do with their “length” when drawn. While it is possible to draw a graph such that the edge’s length is proportional to its weight, this is not done in practice because it makes the drawing quite challenging in general. Rather, we just put a number alongside the edge indicating its weight.
Fig. 7.77 A weighted graph.#
The solution to the traveling salesperson problem for Fig. 7.77 is:
7.4.3. Exercises#
Exercise 7.9
For each of the below graphs, does an Euler circuit exist? If so, give it. If not, does an Euler path exist? If so, give it.
Solution to Exercise 7.9
\(G_1\) has many Euler circuits. One is:
\(G_2\) does not have any Euler circuits. But, it has many Euler paths. One is: