7.1. Graphs

Let’s jump right in with the formal definition of a graph.

Definition (graph)

A graph is a pair \((V,E)\) consisting of a non-empty set of vertices \(V\) and a set of edges \(E\). \(E\) is a subset of the set \(\{ \{u,v\} \ |\ u,v \in V\}\).

In this definition, \(V\) can be any set of discrete elements. Often, it is a subset of the natural numbers. On the other hand, the definition of \(E\) needs some parsing. \(E\) is a set of subsets of \(V\). That is, \(E \subset \mathcal{P}(V)\).

Each of the elements of \(E\) have:

1. two elements, for example \(\{u,v\}\), where \(u,v \in V\), or

2. one element, for example \(\{v,v\} = \{v\}\) for some vertex \(v \in V\).

Fig. 7.2 A graph of \(5\) vertices.

In Fig. 7.2, we have a graph with \(5\) vertices and \(5\) edges.

\[ V = \{1,2,3,4,5\} \qquad E = \{\{1,3\}, \{3,4\}, \{1,4\}, \{4,5\}, \{2,4\}\} \]

Checkpoint

Draw a graph

Draw the graph \((V,E)\) for \(V = \{1,2,3,4\}\) and \(E = \{ \{1,2\}, \{3,4\}, \{4,1\} \}\).

Solution

Draw a graph

Did your graph look different from that of the checkpoint’s solution?

That’s okay! In the definition of a graph we only care about the vertices and the edges connecting them. There is absolutely no rules for how to draw the graphs. The positions of vertices, the lengths of edges, etc. are all up to personal choice.

The following are all the same graph \(G = (V,E)\).

---

7.1.1. The Language of Graphs

As with any new topic, we have a lot of terminology to learn and differentiate between. Here’s a lightning round of terms to remember.

• A simple graph is what we have defined already as a graph. There is at most one edge between any two vertices.

• A multigraph is what we call a graph which allows multiple edges between vertices.

• A node or vertex is a discrete object of the graph.

• The two vertices of an edge are called endpoints. That edge is said to join or connect the two vertices and the edge is incident to each of the vertices it joins.

• When two vertices are joined by an edge, those vertices are called adjacent.

• An edge which connects a vertex to itself is called a loop.

• In some contexts, simple graphs do not allow loops. Our definition does allow loops.

Attention

There is no standard terminology in graph theory. In this course and book we allow a graph to have loops. In other contexts, some people differentiate between graphs without loops and with loops as simple graphs and pseudographs, respectively.

In many many contexts of computer science, graphs with loops are very useful. Thus, we will allow our simple graphs to have loops.

With the correct language to speak about graphs, we can consider more formal definitions.

Definition (order of a graph)

A graph \(G = (V,E)\) of order \(n\) has \(|V| = n\).

Definition (neighbourhood)

The neighbourhood of a vertex \(v\), \(N(v)\), of a graph \(G = (V,E)\) is the set of all vertices adjacent to \(v\) in \(G\).

\[ N(v) = \{u \ |\ \{u,v\} \in E\} \]

Definition (degree of a vertex)

The degree of a vertex \(v\), \(deg(v)\), is the number of edges incident with it. Note that a loop contributes 2 to its degree.

Let’s apply these new definitions to an example. Can you list the degrees and neightbourhoods of every vertex in the graph below?

Counts of a graph

In this graph \(G\) we have:

• The order of \(G\) is \(6\).

• The degree of \(3\) is \(3\).

• The degree of \(5\) is \(1\).

• The degree of \(6\) is \(3\).

• The neightbourhood of \(3\) is \(\{2,4,6\}\)

• The neightbourhood of \(6\) is \(\{1, 3, 5\}\)

• And many more facts of the degree and neighbourhoods of other vertices…

There is a fun theorem connecting the degree of vertices in a graph to its number of edges.

The Handshake Theorem

If \(G = (V,E)\) is a graph with \(m\) edges, then:

\[ 2m = \sum_{v\in V} deg(v) \]

Proof: Each edge contributes twice to the degree count of all the vertices in the graph. Indeed, each edge is incident to exactly two vertices. \(\{u,v\} \in E\) contributes \(1\) to both \(deg(u)\) and \(deg(v)\).

Thus, it must be that \(\sum_{v \in V} deg(v)\) is twice the total number of edges. \(\blacksquare\)

The handshake theorem actually leads to a very interesting theory about graphs.

Theorem

A graph \(G = (V,E)\) always has a an even number of vertices with odd degree.

Proof: Partition the set of vertices \(V\) into \(V_1\), all vertices with even degree, and \(V_2\), all vertices with odd degree. By the handshake theorem we have:

\[\begin{split} 2m &= \sum_{v\in V} deg(v) \\ &= \sum_{v \in V_1} deg(v) + \sum_{v \in V_2} deg(v) \\ \end{split}\]

The left-hand side of this equation, \(2m\) is obviously even. Since each \(v\) in \(V_1\) has even degree, and the sum of even numbers is even, then \(\sum_{v \in V_1} deg(v)\) is also an even number.

The only way for an even number plus another number to be equal to an even number is if the other number is even. Thus, \(\sum_{v \in V_2} deg(v)\) is an even number.

But, each \(v\) in \(V_2\) has odd degree. How can the sum of odd numbers be even? Only when the number of numbers in the sum is even. Thus, there must be an even number of vertices with odd degree. \(\blacksquare\)

Before we get into studying graphs with special properties, let’s make sure we have a good understanding of the basic terminology of graphs.

Checkpoint

Terminology of a graph

Consider the following graph and answer the below questions.

Fig. 7.3 A graph with a loop.

1. What is the order of this graph?

2. How many edges are in this graph?

3. What is the neighbourhood of \(5\)?

4. Which vertices are adjacent to \(3\)?

5. What is the degree of vertex \(2\)?

6. What is the degree of vertex \(7\)?

7. What is the neighbourhood of \(7\)?

Solution

Terminology of a graph

\(\ \)

Fig. 7.4 A graph with a loop.

1. \(7\)

2. \(7\)

3. \(\{6\}\)

4. \(2\) and \(4\)

5. \(3\)

6. \(2\)

7. \(\{7\}\)

---

Sub-Graphs and Induced Graphs

Much like sets and subsets, we have graphs and subgraphs. Formally, a subgraph is as follows.

Definition (subgraph)

A subgraph of a graph \(G = (V,E)\) is another graph \((W,F)\) such that \(W \subseteq V\) and \(F \subseteq E\). A proper subgraph of \(G\) if \(W \subsetneq V\).

Notice in this definition that we require the sets \(W\) and \(F\) to form a \(graph\). Thus, there cannot be edges in \(F\) whose endpoints are not also in \(W\).

Fig. 7.5 \(G_1\)

Fig. 7.6 \(G_2\)

Fig. 7.7 \(G_3\)?

The left-most graph \(G_1\) is a simple graph with \(5\) vertices and \(6\) edges: \(\{1,2,3,4,5\}\) and \(\{\{1,2\}, \{2,4\}, \{4,5\}, \{5,3\}, \{3,2\}, \{2,5\}\}\).

The \(G_2\) is a proper subgraph of \(G_1\). It has vertices \(\{2,3,5\}\) and edges \(\{ \{2,3\}, \{3,5\}\}\).

However, \(G_3\) is not a graph. It has an edge with no endpoint! Since \(G_3\) is not a valid graph, it cannot be a subgraph of \(G_1\).

A special kind of subgraph is an induced subgraph. In an induced graph we only care about the subset of vertices, and take every edge from the original graph whose endpoints are still in the subset of vertices.

Definition (induced graph)

For a graph \(G = (V,E)\) and a set of vertices \(W \subseteq V\), a subgraph induced by \(W\) is the graph \((W,F)\) where an edge is in \(F\) if and only if \(\{u,v\} \in E\) for \(u,v \in W\).

In Fig. 7.6, \(G_2\) is not an induced subgraph because it is missing the edge \(\{2,5\}\) of the original graph \(G_1\).

Fig. 7.8 The subgraph induced by \(\{2,3,5\}\) of \(G_1\) from Fig. 7.5.

---

7.1.2. Connectivity

Arguably the most important thing about graphs is that that they encode connections. Recall that the definition of a graph only requires vertices and connections (edges) between them. We don’t care about the placement of vertices or the length of edges, or even if edges overlap.

All we care about in a simple graph is whether two vertices are adjacent or not.

Understanding whether two vertices are connected is the study of connectivity.

Definition (path)

A path of a simple graph \(G = (V,E)\) is a sequence of vertices \((v_n)\) where an edge exists between \(v_i\) and \(v_{i+1}\) for \(1 \leq i < n\).

As a consequence of a path, we have an alternative definition for adjacent vertices. Two vertices are adjacent if they are connected with a path of length \(1\).

From paths we get a formal definition of connectivity.

Definition (connected)

Two vertices \(u, v\) in a graph are connected if there exists a path from \(u\) to \(v\). Otherwise, \(u\) and \(v\) are said to be disconnected. A graph is connected if every pair of vertices in the graph is connected.

The above graph has many paths. And, in particular, every vertex is connected to every other vertex. Thus, the graph is a connected graph. In contrast, the graph in the previous checkpoint Fig. 7.3 is disconnected.

We also have useful terminology around paths in a graph:

1. When a path begins and ends at the same vertex it is called a circuit

2. A path \((v_1, v_2, \ldots, v_n)\) is said to pass through the vertices \(v_2, v_3, \ldots, v_{n-1}\) and traverse the edges \(\{v_1,v_2\}, \{v_2, v_3\}, \ldots, \{v_{n-1}, v_n\}\).

3. A path is simple if every edge in the path only appears once.

4. When a path exists between \(u\) and \(v\), we say that \(v\) is reachable from \(u\).

Fig. 7.9 A graph with 3 unique cycles.

Fig. 7.10 A graph with 3 unique cycles.

Remember that graphs are all about connectivity. Thus, the graphs in Fig. 7.9 and Fig. 7.10 are actually the same graph, just drawn differently.

From Fig. 7.10, it is easier to see that this graph has three unique cycles (up to a choice of starting point and direction of travel):

\[\begin{split} &2, 4, 5, 1, 3, 2 \\ &2, 3, 1, 6, 2 \\ &2, 4, 5, 1, 6, 2 \\ \end{split}\]

---

Graph Isomorphisms

Two graphs may be the same graph, just drawn differently, as we have just seen. However, Some graphs are “almost” the same and not just drawn differently. It could be that there are different labels on the vertices, for example.

Whether two graphs are actually the exact same, but just drawn differently, or are “almost” the same, we can formally describe graphs as being “sufficiently similar” by isomorphisms.

Definition (isomorphic graphs)

Two simple graphs \(G_1 = (V_1, E_1)\) and \(G_2 = (V_2, E_2)\) are isomorphic if there exists a bijection function \(f\) from \(V_1\) to \(V_2\) with the property that two vertices \(v_1, u_1 \in V_1\) are adjacent in \(G_1\) if and only if \(f(v_1)\) and \(f(u_1)\) are adjacent in \(G_2\). The bijective function \(f\) is called an isomorphism.

From the definition of isomorphic graphs, it is obvious that two graphs \(G_1 = (V_1, E_1)\) and \(G_2 = (V_2, E_2)\) must have \(|V_1| = |V_2|\) and \(|E_1| = |E_2|\) to be isomorphic. But this is not enough, adjacencies must be maintained as well.

Fig. 7.11 Two isomorphic graphs.

In these above two graphs, call the left \(G_1\) and right \(G_2\). Can we find a bijection between these graphs?

\[ f(1) = a, \quad f(2) = b, \quad f(3) = d, \quad f(4) = c \]

This bijection works because:

1. \(1\) is connected to \(2\) and \(3\) in \(G_1\) and \(f(1) = a\) is connected to \(f(2) = b\) and \(f(3) = d\) in \(G_2\).

2. \(2\) is connected to \(1\) and \(3\) in \(G_1\) and \(b\) is connected to \(a\) and \(d\) in \(G_2\).

3. \(3\) is connected to \(1\), \(2\), and \(3\) in \(G_1\) and \(d\) is connected to \(a\), \(b\), and \(f(4) = c\) in \(G_2\).

4. \(4\) is connected to \(3\) in \(G_1\) and \(c\) is connected to \(d\) in \(G_2\).

Note that there may be several possible bijections between the same two graphs. Two graphs are isomorphic as long as there is at least one bijection between them.

Checkpoint

Graph isomorphisms

Consider Fig. 7.11 again. Find a bijection between the two graphs which is different from the bijection given above.

Solution

Graph isomorphisms

\[ f(1) = b, \quad f(2) = a, \quad f(3) = d, \quad f(4) = c\ \]

Notice that \(f(3)\) and \(f(4)\) remain the same between this and the previous bijection. Why? Because of the structure of the graph itself. In both graphs \(4\) and \(c\) are the only vertices of degree 1. Thus, any bijection between the two graphs must map \(4\) to \(c\). Similarly, \(3\) and \(d\) are the only vertices of degree \(3\), so any bijection between the two graphs must map \(3\) to \(d\).

When there are a small number of vertices in two graphs, it is easy to determine by inspection if they are isomorphic or not. But, for large graphs, doing so is very hard. For a graph with \(n\) vertices, the best known algorithm has a time complexity of \(2^{O((\log n)^3)}\) to determine if if two graphs with \(n\) vertices are isomorphic.

Visually, one way we can determine if two graphs are isomorphic are by “dragging” the vertices around. To try and get one to match the other.

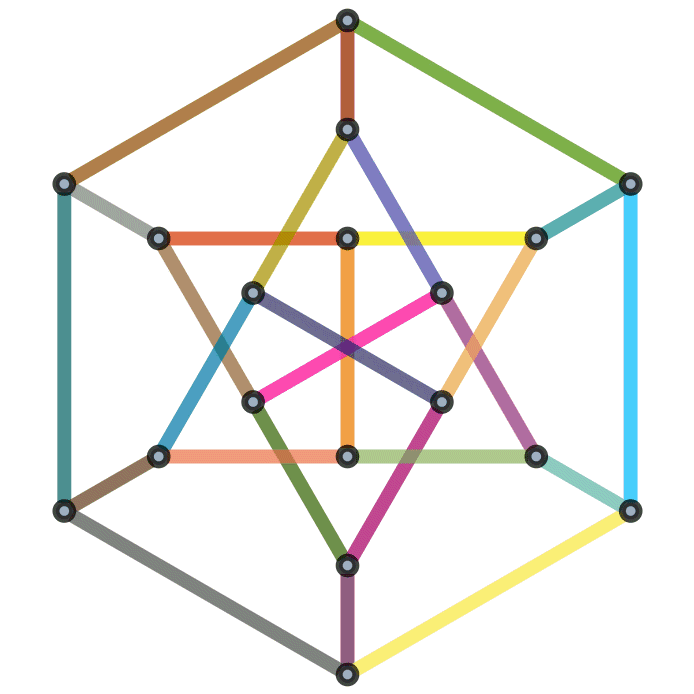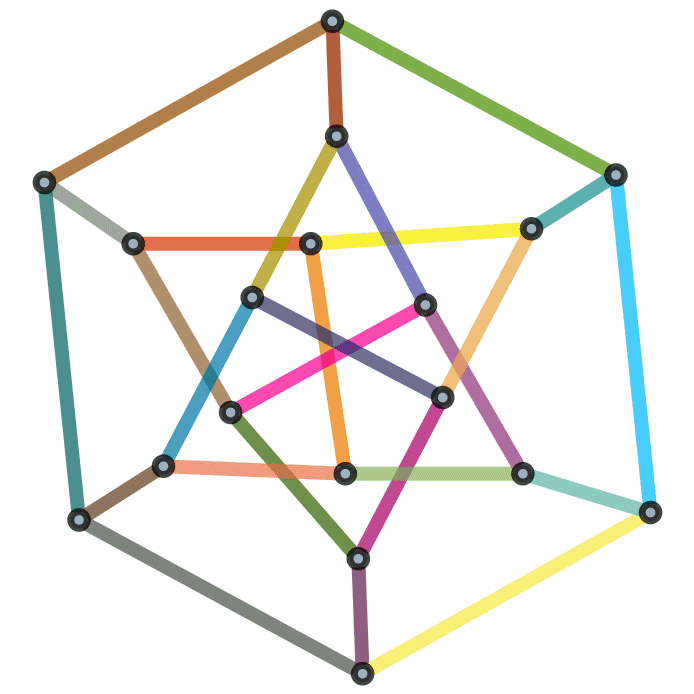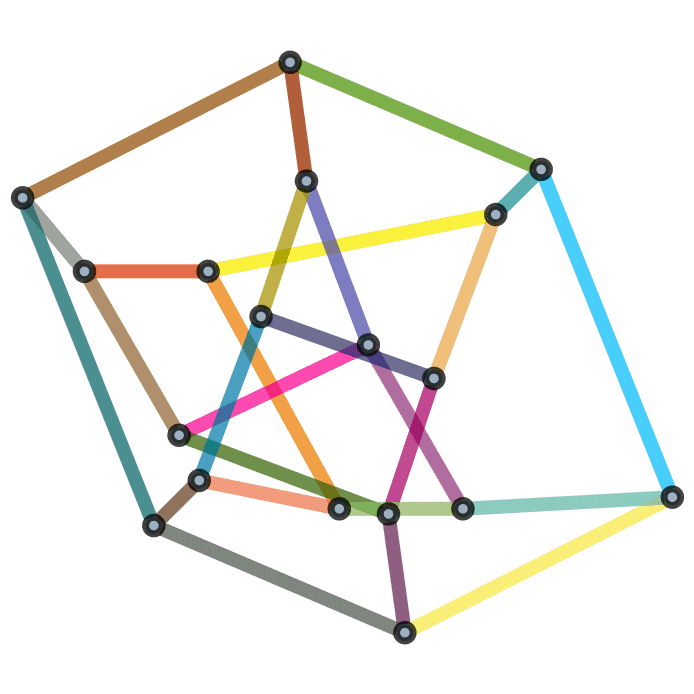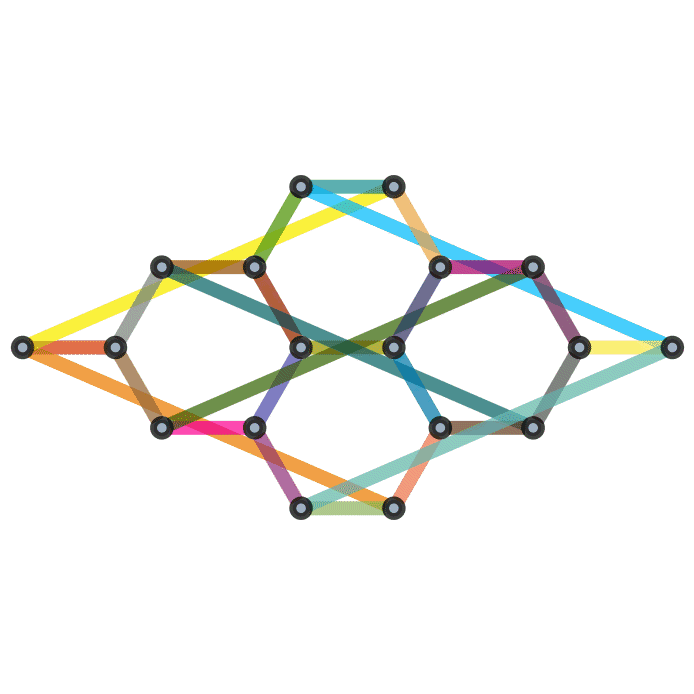
Fig. 7.12 An animation showing two graphs are isomorphic. From Michael Sollami.

---

Connected Components

In large graphs, it is very common for the graph to not be connected. That is, there pairs of vertices for which no path exists between them.

Fig. 7.13 A graph with \(9\) vertices and \(8\) edges.

The graph in Fig. 7.13 is not connected, but it does have \(3\) connected components.

Definition (connected component)

An induced subgraph \(H = (W,F)\) of a graph \(G = (V,E)\) is a connected component if \(H\) is a connected graph and adding any other vertex \(v \in V \setminus W\) would make \(H\) disconnected.

There are two ways to think of connected components:

1. A component component \(H\) is a connected subgraph of a graph \(G\) where no other connected subgraph of \(G\) exists for which \(H\) is also a subgraph.
   

   In Fig. 7.13 the subgraph induced by \(\{3,4,8\}\) is a connected component. The subgraph induced by \(\{3,4\}\) is connected, but it also a subgraph of the subgraph induced by \(\{3,4,8\}\). Thus, \(\{3,4\}\) is not a maximal connected subgraph.

2. Given a graph \(G = (V,E)\), choose a vertex \(v \in V\). The connected component of \(v\) is the subgraph induced by all vertices reachable from \(v\). That is, all the vertices for which a path exists starting from \(v\).

Finding connected components

Fig. 7.14 A graph with \(9\) vertices.

In the above graph, which vertices are reachable from \(4\)? How many connected components are there in the graph? How many edges are there in the connected component containing \(2\)?

1. \(4\), \(5\), \(8\), and \(9\) are all reachable from \(4\).

2. There are \(2\) connected components in this graph.

3. The connected component containing \(2\) has \(5\) edges. Connected components must be maximal with respect to vertices and edges.

Reachability can be formalized recursively using neighbourhoods. Let \(R(v)\) be the set of vertices reachable from \(v\):

\[\begin{split} &v \in R(v), \text{ and} \\[1em] &\text{if } u \in R(v) \text{ then } N(u) \subseteq R(v). \end{split}\]

Reachability of a vertex \(v\) is the transitive closure of the neighbourhood of \(v\).

Consider again Fig. 7.14. What is \(R(2)\)?. \(2\) itself is in \(R(2)\). Then, \(N(2)\) is a subset of \(R(2)\), so \(6\) and \(7\) are in \(R(2)\). Thus, the neighbourhoods of \(6\) and \(7\) are also in \(R(2)\). This adds \(3\) to \(R(2)\). Then, the neighbourhood of \(3\) is also in \(R(2)\) which adds \(1\). Finally, there are no more neighbours to add. The connected component containing \(2\) is the subgraph induced by \(R(2) = \{1, 2, 3, 6, 7\}\).

---

Connected Components as an Equivalence Relation

Reachability actually defines an equivalence relation on a graph. Indeed, you can see visually that the vertices of a graph are partitioned into connected subgraphs.

Fig. 7.15 A graph with \(3\) connected components.

The vertices in the graph of Fig. 7.15 are partitioned into three sets: \(\{7,9\}\), \(\{2, 4, 8\}\), and \(\{1,2,5,6\}\) where the induced subgraph of each of these partitions is a connected graph.

Can we show that reachability defines an equivalence relation? Of course!

Reachability is an equivalence relation

Let \(G = (V,E)\) be a graph. For \(u,v \in V\), let \(u \sim v\) when \(v\) is reachable from \(u\).

1. Reflexive. Every vertex is reachable from itself. Therefore \(v \sim v\) for every \(v \in V\).

2. Symmetric. If \(u \sim v\) then \(v\) is reachable from \(u\). Thus a path exists from \(u\) to \(v\). Thus, a path also exists from \(v\) to \(u\) and \(v \sim u\).

3. Transitive. If \(u \sim v\) and \(v \sim w\), then \(v\) is reachable from \(u\) and \(w\) is reachable from \(v\). Thus, a path exists from \(u\) to \(v\) and \(v\) to \(w\). Thus, a path exists from \(u\) to \(w\) by simple joining the two paths from \(u\) to \(v\) and \(v\) to \(w\). Thus, \(u \sim w\).

---

Complete Graphs

A complete graph is a special kind of connected graph. Not only must the graph be connected—there must be a path from every vertex toe very other vertex—but each path must be of length \(1\). That is, every vertex must be adjacent to every other vertex.

Definition (complete graph)

A complete graph is a graph where every one of its vertices is adjacent to every other vertex. A complete graph of order \(n\) is denoted \(K_n\).

Fig. 7.16 The complete graphs \(K_1\), \(K_2\), \(K_3\).

A graph containing a single vertex is complete (vacuously so). A graph containing two vertices connected by a single edge is also complete. A graph of three connected into a triangle is also complete.

The first complete graphs are rather simple, but they quickly grow to be very complex.

Fig. 7.17 \(K_4\)

Fig. 7.18 \(K_5\)

Fig. 7.19 \(K_6\)

Why are these so complex? Precisely because of the definition of a complete graph. There must an edge between every pair of vertices. Of course, we can count how many edges there will be.

Theorem

A complete graph of order \(n\) has \(\frac{n(n-1)}{2}\) edges.

Proof: A complete graph has an edge between any two vertices. For a graph with \(n\) vertices, if we choose any two vertices there must be an edge between them. There are \(\binom{n}{2}\) such choices.

\[ \binom{n}{2} = \frac{n!}{(n-2)!2!} = \frac{(n-1)(n)}{2}. \qquad\qquad \blacksquare \]

Cliques

Complete graphs are very special graphs. There’s not many of them. Indeed, for a positive integer \(n\) there is exactly one complete graph of order \(n\), up to isomorphism. It is \(K_n\).

What is more common is a clique, a special kind of subgraph.

Definition (clique)

For a graph \(G = (V,E)\) a clique is an induced subgraph of \(G\) that is complete.

Definition (maximal clique)

A maximal clique of \(G = (V,E)\) is a clique that cannot be made larger by including any other adjacent vertex of \(V\).

Notice that a complete graph of order \(n\) is trivially a clique of size \(n\).

Consider Fig. 7.14, show again below.

This graph has many cliques of size 2. Indeed, any pair of vertices connected by an edge forms a clique. Every vertex by itself also creates a clique.

Most often we consider cliques of size \(3\) or greater. In the case of this graph, the only clique of size \(3\) is \(\{2,6,7\}\). Moreover, this clique is maximal since adding the only other adjacent vertex, \(3\), would make the induced subgraph on longer complete.

Checkpoint

Finding Cliques

Find all cliques of size \(3\) or more in the above graph. Which are maximal?

Solution

Finding Cliques

1. \(\{a,c,d\}\)

2. \(\{d,e,f\}\)

3. \(\{b,c,d,e\}\)

4. \(\{b,c,d\}\)

5. \(\{b,d,e\}\)

6. \(\{c,d,e\}\)

7. \(\{b,c,e\}\)

\(\{a,c,d\}\), \(\{d,e,f\}\), \(\{b,c,d,e\}\) are maximal

From this above checkpoint, notice that any clique of size \(n\) also contains a many cliques of size \(n-1\), many cliques of size \(n-2\), and so on.

Cliques are very useful and powerful properties. Think about what a clique could represent. If the graph is represents a collection of friendships, then a clique is a true “clique of friends”. If the graph is a compute network, then every computer in a clique has a direct connection to any other computer in the clique.

---

7.1.3. Special Graphs

We have already seen complete graphs as a special graph with a special name. There are many other useful useful graphs with special names and different properties.

Cycles

Definition (cycle graph)

A cycle graph is a graph with exactly one cycle. The cycle graph of order \(n\) is denoted \(C_n\).

As a consequence of cycles, a cycle graph must have \(3\) or more vertices.

Fig. 7.20 \(C_3\)

Fig. 7.21 \(C_4\)

Fig. 7.22 \(C_5\)

Fig. 7.23 \(C_6\)

---

Wheels

Definition (wheel graph)

A wheel graph is a cycle graph in which one extra vertex has been added which connects to every other vertex in the cycle. The wheel graph of order \(n\) is denoted \(W_n\).

We call these “wheels” because the look like a wheel: a central hub and a tire or rim. The single vertex connected to every other is the “hub”. The cycle is the “rim”

Fig. 7.24 \(W_4\)

Fig. 7.25 \(W_5\)

Fig. 7.26 \(W_6\)

Notice that \(W_n\) is \(C_{n-1}\) with the added hub vertex. Moreover, notice that \(W_4\) is the same as \(K_4\).

---

Planar Graphs

Definition (planar graph)

A planar graph is a graph that can be drawn with no overlapping edges.

Planar graphs have many nice properties and theorems associated with them. See, for example, wikipedia.

For our purposes in this text, planar graphs are nice because they’re simply easy to draw and understand.

Most of the graphs we’ve seen so far are planar. Every cycle graph is planar. Every wheel graph is planar. In contrast, every complete graph of order \(5\) or higher is not planar.

Fig. 7.27 \(W_6\) is planar.

Fig. 7.28 \(C_6\) is planar.

Fig. 7.29 \(K_4\) is planar, even if it does not look like it.

An important note about planar graphs is that just because they can be drawn with overlapping edges, does not mean that they are necessarily not planar.

\(K_4\) is planar even though its typical way of drawing has crossed edges. Indeed, \(K_4\) and \(W_4\) are the same graph, and \(W_4\) is obviously planar.

Fig. 7.30 \(K_4\) is planar.

Fig. 7.31 \(W_4\) is planar.

So, a graph is planar if there is at least one way of drawing it so that there are no crossed edges.

---

Bipartite Graphs

Definition (bipartite graph)

A bipartite graph is a graph \(G = (V,E)\) whose vertices can be partitioned into two disjoint sets \(V_1\) and \(V_2\) such that every edge in \(E\) has one endpoint int \(V_1\) and one endpoint in \(V_2\).

In a bipartite graph with vertices partitioned into \(V_1\) and \(V_2\), there cannot be any edges within a partition.

Fig. 7.32 \(C_4\) is a bipartite graph

\(C_4\) is a bipartite graph because its vertices can be partitioned into two groups so that are no edges within either partition. In the case of \(C_4\), opposite corners are in the same partition, as indicated by the coloring above.

Bipartite graphs are highly related to the problem of graph coloring. Graph coloring is just some way of labeling or grouping vertices. Since graphs are highly visual, we usually use colors. But, “coloring” can mean any form of labeling of vertices.

Proposition

A graph is bipartite if its vertices can be colored using exactly two colors so that now two adjacent vertices have the same color.

Fig. 7.33 A bipartite graph \(G\).

Fig. 7.34 A coloring of \(G\) with two colors.

Fig. 7.35 Moving the vertices of Fig. 7.34 to explicitly show edges between colors.

Theorem

A simple graph is a bipartite graph if and only if it does not contain any cycles of odd length.

A full proof is left to the reader. However, observer that any graph with a cycle of length \(3\) cannot be bipartite. Why? Proceed by contradiction. Suppose a bipartite graph had a cycle with length \(3\). In a bipartite graph every step along an edge must take you from one of the partitions to another. Call these partitions \(V_1\) and \(V_2\).

W.l.o.g. say you start at a vertex \(v\) in \(V_1\) which is also part of a cycle of length three. Take one step along that cycle and you must be in \(V_2\). Take another cycle along that cycle and you must be in \(V_1\). Taking another step along that cycle, you should be in \(V_2\), since the graph is assumed to be bipartite. However, because the cycle is of length three, after \(3\) steps you are back at the starting point \(v\). But, \(v \in V_1\). Hence, the assumption that the graph is bipartite must be false.

Fig. 7.36 A graph with a cycle of length \(3\) cannot be bipartite.

---

Complete Bipartite Graphs

Imagine a bipartite graph with two cliques. That’s a complete bipartite graph!

Definition (complete bipartite graph)

A complete bipartite graph is a bipartite graph whose vertices can be partitioned into two sets \(V_1\) and \(V_2\) and there is an edge for every vertex in \(V_1\) to every vertex in \(V_2\). Where \(|V_1| = m\) and \(|V_2| = n\), The complete bipartite graph is denoted \(K_{m,n}\).

Fig. 7.37 \(K_{3,3}\)

Fig. 7.38 \(K_{3,4}\)

Fig. 7.39 \(K_{5,3}\)

Notice that, up to a choice of coloring, \(K_{m,n}\) and \(K_{n,m}\) are the same graph.

Fig. 7.40 \(K_{5,7}\)

Fig. 7.41 \(K_{7,5}\)

---

7.1.4. Trees

Trees are an extra special type of graph that are worthy of their own section.

Indeed, you could have an entire course talking about just trees. There’s things like spanning trees, binary trees, quadtrees, and octrees.

Definition (tree)

A tree is a simple connected graph with no cycles.

Sounds simple, right? With such a simple definition comes a lot of flexibility and power to describe things.

Fig. 7.42 A tree with 9 vertices.

In fact, we have many equivalent definitions of trees. You could think of them as properties of trees.

1. If any new edge is added to a tree, then a cycle is formed.

2. If any edge is removed from a tree, then the graph becomes disconnected.

3. A connected graph with \(n\) vertices and \(n-1\) edges is a tree.

4. Any two vertices in a tree have a unique simple path between.

You will see trees everywhere in computer science. However, most trees in computer science are a special kind of tree called a rooted tree.

---

Rooted Trees and Children

Definition (rooted tree)

A rooted tree is a tree in which one of the vertices has been designated as the root.

Why are rooted trees important? Because it gives us a canonical view of the tree. Consider the tree in Fig. 7.42. We could choose \(1\) to be the root (shown on the left below) or choose \(3\) to be the root (shown on the right below).

Fig. 7.43 A tree rooted at \(1\).

Fig. 7.44 A tree rooted at \(3\).

Designating a root in a tree induces special relationships between vertices. It derives from that fact that there is a unique simple path from any vertex to any other vertex in a tree. The terminology used most commonly is based on ancestry.

• The root is the “oldest” ancestor.

• Each of the children of the root are the vertices which have a path of length 1 from the root.

• The children of those children are vertices which have a path of length 2 from the root.

• Conversely, the children of the root tree have the root as their parent.

• To speak about a vertex’s children and children’s children, etc. we say descendants.

Consider Fig. 7.43. \(1\) is the root. Its children are \(2,3\). The children of \(3\) are \(7,8\), the child of \(8\) is \(9\), and so on. Now consider Fig. 7.44. Here, \(3\) is the root. As such, \(1\) is now a child of \(3\).

Visually, rooted trees are almost always drawn with the root at the top. Then, children are always drawn lower than their parents (think of Hasse Diagrams).

If we wanted to be very precise with the drawing of a rooted tree, we would draw every child at the same level of a tree at the same y-position. The level of a vertex in a tree is its distance from the root.

Fig. 7.45 A “properly drawn” tree rooted at \(3\).

A very important property of tree is that they admit a recursive description. For every non-root vertex \(v\) in a tree, there is a subtree rooted at \(v\).

Definition (rooted subtree)

Given a non-root vertex \(v\) of a rooted tree, the subtree rooted at \(v\) is the subgraph rooted at \(v\) and induced by \(v\) and all its descendants.

Fig. 7.46 Three subtrees of Fig. 7.45: the subtree rooted at \(7\), the subtree rooted at \(8\), and the subtree rooted at \(2\).

---

Binary Trees

A binary tree is perhaps the most important tree structure in computer science.

Definition (binary tree)

A binary tree is a rooted tree where each vertex has at most \(2\) children. A full binary tree is a binary tree where every vertex has exactly \(2\) children or \(0\) children.

Therefore, Fig. 7.45 is not a binary tree. The vertex \(3\) has three children!

Fig. 7.47 A binary tree.

Fig. 7.48 A full binary tree.

Thinking back to Recursive Definitions, binary trees lend themselves very naturally to a recursive definition.

Consider the following recursive definition of the set of all possible full binary trees.

• Basis step: A single vertex \(r\) is the root of a full binary tree.

• Recursive Step: Let \(T_1\) and \(T_2\) be binary trees with roots \(r_1\) and \(r_2\). Let \(r\) be a new vertex which is not in \(T_1\) or \(T_2\). Add an edge from \(r\) to \(r_1\) and from \(r\) to \(r_2\). The resulting graph is a full binary tree rooted at \(r\).

Fig. 7.49 Recursively constructing a full binary tree where \(r_1\) and \(r_2\) may not have children.

Fig. 7.50 Recursively constructing a full binary tree where \(r_1\) and \(r_2\) each have at least two descendants.

Fig. 7.51 Recursively constructing a full binary tree where \(r_1\) has at least two descendants.

Via this recursive definition and the above figures, we can see that given any number of full binary trees, we can construct new binary trees by connected two at a time to some new root vertex.

This recursive definition trees extends beyond just their construction to also describe some of their properties. As we will see next with structural induction.

---

Structural Induction

We have already seen mathematical induction, strong induction, and the well-ordering principle. Now, structure induction is a specialization of mathematical induction to the context of recursively-defined structures.

We’ve seen recursively defined sets previously, and we have just seen recursively defined binary trees. The goal now is to use induction to prove some properties on these recursive definitions.

Much like mathematical induction, structural induction has a basis step, an inductive step, and an inductive hypothesis.

Structural Induction

1. Basis step: Show that the desired property is true for all elements specified in the basis step of the recursive definition.

2. Inductive step: Assume that the desired property is true for all of the old elements which are used to construct new elements. Then, show that the desired property must also hold for the new elements.

Let’s start with a more familiar example rather than trees.

Structural induction on the integers

Let the set of integers \(\mathbb{Z}\) be defined recursively as:

1. \(0 \in \mathbb{Z}\)

2. For \(x \in \mathbb{Z}\), \(x + 1 \in \mathbb{Z}\) and \((-1)(x) \in \mathbb{Z}\).

Show that the absolute value of any integer is a natural number.

Proof: Proceed by structural induction.

Base case: \(|0| = 0\) is a natural number.

Inductive Step: Let \(x \in \mathbb{Z}\) and assume \(|x| \in \mathbb{N}\). By the recursive definition we also have \(x + 1 \in \mathbb{Z}\) and \((-1)x \in \mathbb{Z}\). We look to show that \(|x+1| \in \mathbb{N}\) and \((-1)x \in \mathbb{N}\).

Let \(x\) be non-negative. Then \(|x+1| = |x| + 1\), and \(|x|\) is assumed to be a natural number, then \(|x| + 1\) is a natural number. If \(x\) is negative then \(|x+1| = |x| - 1\). Again, \(|x|\) is assumed to be a (positive) natural number, and thus so is \(|x| - 1\). Thus, \(|x+1|\) is a natural number.

Since \(|(-1)x| = 1|x| = |x|\), and we assume \(|x| \in \mathbb{N}\) by the inductive hypothesis, \(|(-1)x|\) must also be a natural number.

Hence, by structural induction, for all \(x \in \mathbb{Z}\), \(|x| \in \mathbb{N}\). \(\blacksquare\)

To apply structural induction to trees, let’s first define some properties on binary trees.

Definition (binary tree height)

The height of a rooted binary tree \(T\), denoted \(h(T)\), is the maximal length of any simple path in the tree with the root as one of its endpoints.

Let us prove the following theorem by structural induction.

Theorem

For a full binary tree \(T = (V,E)\), \(|V| \leq 2^{h(T)+1} -1\).

Proof: Proceed by structural induction.

Base case: A single vertex is a full binary tree. Thus \(|V| = 1\) and its height is 0. Thus, \(|V| = 1 \leq 2^{1} - 1\).

Inductive step: Suppose that the inequality holds for any two full binary trees \(T_1 = (V_1, E_2)\) and \(T_2 = (V_2, E_2)\). Following the recursive definition, we construct a new binary tree \(T\) by joining the roots of \(T_1\) and \(T_2\) to a new vertex \(r\).

Clearly, the number of vertices in \(T\) is \(|V_1| + |V_2| + 1\).

Notice also that in the construction of \(T\), any path in \(T_1\) starting at its root can be extended to start at \(r\), the new root, by adding the newly constructed edge connecting the two. The same holds for \(T_2\). Therefore, the height of \(T\) must be \(h(T) = \max(h(T_1), h(T_2)) + 1\).

Therefore, we look to show that \(|V_1| + |V_2| + 1 \leq 2^{h(T)+1} -1\).

\[\begin{split} |V_1| + |V_2| + 1 &\leq (2^{h(T_1)+1} - 1) + (2^{h(T_2)+1} - 1) + 1 \qquad \text{by inductive hypothesis} \\[1em] &= 2^{h(T_1)+1} + 2^{h(T_2)+1} - 1 \\[1em] &\leq 2 \cdot \max(2^{h(T_1)+1}, 2^{h(T_2)+1}) - 1 \\[1em] &= 2\cdot 2^{\max(h(T_1), h(T_2)) + 1} - 1 \\[1em] &= 2^{\max(h(T_1), h(T_2)) + 1 + 1} - 1 \\[1em] &= 2^{h(T)+1} - 1 \end{split}\]

Therefore, by structural induction, for any full binary tree \(T = (V,E)\), \(|V| \leq 2^{h(T)+1} - 1\). \(\blacksquare\).

Now, can you prove one yourself?

Checkpoint

Number of vertices and edges in a binary tree

Prove the following proposition using the recursive definition of full binary trees from Binary Trees.

Proposition

For any full binary tree \(T = (V,E)\), \(|V| = |E| + 1\).

Solution

Number of vertices and edges in a binary tree

Proof: Proceed by structural induction.

Base case: a single vertex is a full binary tree. There, \(|V| = 1, |E| = 0\). Thus, \(|V| = |E| + 1\), as desired.

Inductive step: Suppose that for any two full binary trees \(T_1 = (V_1, E_2)\) and \(T_2 = (V_2, E_2)\) we have \(|V_1| = |E_1| + 1\) and \(|V_2| = |E_2| + 1\).

Following the recursive definition, we construct a new binary tree \(T\) by joining the roots of \(T_1\) and \(T_2\) to a new vertex \(r\). In this new tree we have added one vertex and two edges. Thus, we have the number of vertices in the new tree is \(n = |V_1| + |V_2| + 1\). The number of edges in the new tree is \(m = |E_1| + |E_2| + 2\).

By the inductive hypothesis we have:

\[\begin{split} n = |V_1| + |V_2| + 1 &= (|E_1| + 1) + (|E_2| + 1)+ 1 \\[1em] &= (|E_1| + |E_2| + 2) + 1 \\[1em] &= m + 1 \end{split}\]

Thus, the formula holds for the newly constructed tree. Hence, by structural induction, for any binary tree \(T = (V,E)\) we have \(|V| = |E| + 1\). \(\blacksquare\)

---

7.1.5. Optional Readings

Hashed Octrees

If we extend the idea of binary trees to trees with at most \(4\) children or \(8\) children, we get quadtrees and octrees.

Quadtrees and octrees that are used in practice are almost always full. Moreover, they are used to give a hierarchical spacial decomposition. A node in the tree represents some area (for quadtrees) or volume (for octrees) in space. The children of that node represent a regular partition of the space represented by the node. This procedure continues recursively.

In the above figure, the root node in black represents the entire volume. Its children, the blue nodes, represent the \(8\) larger cubes within the black cube. Then, the green nodes represent the \(8\) smaller cubes within a single blue cube.

Irene Gargantini is a Professor Emerita in computer science of the University of Western Ontario. One of her seminal works is on an effective encoding of a quadtrees called a linear quadtree.

This has been extended to octrees and is also called hashed quadtrees.

The actual encoding and power of this representation is beyond the scope of this course. But, it’s a fun fact to know UWO and Dr. Gargantini were at the forefront of this field in the 1980s.

Euler’s Formula

To finish off this section here’s another fun video by 3Blue1Brown. It gives us a nice visualization of graphs, trees, and Euler’ formula:

\[ |V| - |E| + |F| = 2 \]

---

7.1.6. Exercises

Exercise 7.1

Find all simple paths from \(2\) to \(4\) which do not traverse \(2\) or \(4\).

Solution to Exercise 7.1

1. \(2, 1, 4\)

2. \(2, 4\)

3. \(2, 5, 4\)

4. \(2, 3, 5, 4\)

Exercise 7.2

Show that the above two graphs are isomorphic by giving a bijection between them. Show that this bijection maintain adjacencies.

Exercise 7.3

Show that the above graph is bipartite by giving sets \(V_1\) and \(V_2\) which partition the vertices.

Solution to Exercise 7.3

Exercise 7.4

A quadtree is a rooted tree such that each non-leaf node of the tree has up to 4 children. A full quadtree can be defined recursively as follows.

• Base: A single vertex \(v\) is a full quadtree with \(v\) being the root.

• Recursive Step: If \(T_1, T_2, T_3, T_4\) are pairwise disjoint full quadtrees, then a new full quadtree can be formed with a new vertex \(v\) and four edges connecting \(v\) and each root of \(T_1, T_2, T_3, T_4\). \(v\) is the root of the new quadtree.

Let \(n(T)\) be the number of vertices in a quadtree \(T\). Let \(h(T)\) be the height of \(T\), that is, the maximal length of any path in \(T\) with the root of \(T\) as one of the path’s endpoints.

Use structural induction to prove that for a full quadtree \(T\), \(n(T) \geq 4h(T)\).

Solution to Exercise 7.4

The base case of a single node \(v\) has \(n(T) = 1\), \(h(T) = 0\). thus \(1 \geq 4(0) = 1\).

Let \(T_1, T_2, T_3, T_4\) be full quadtrees. Assume that \(n(T_i) \geq 4{h(T_i)}\) for \(1 \leq i \leq 4\). We construct a new quadtree \(T\) be joining \(T_1,T_2,T_3,T_4\) as stated in the recursive step. This new tree clearly has \(n(T) = 1 + n(T_1) + n(T_2) + n(T_3) + n(T_4)\). Moreover, \(h(T) = 1 + \max(h(T_1), h(T_2), h(T_3), h(T_4))\).

W.l.o.g. let \(h(T_1)\) the maximal one. Thus, \(h(T) = 1 + h(T_1)\). We look to show that \(n(T) \geq 4h(T) = 4 + 4h(T_1)\).

By construction, \(n(T) = 1 + n(T_1) + n(T_2) + n(T_3) + n(T_4)\) with \(n(T_i) \geq 1\) for all \(T_i\). Thus, \(n(T) \geq 4 + n(T_1)\). By inductive hypothesis we have that \(4 + n(T_1) \geq 4 + 4h(T_1)\). Thus, \(n(T) \geq 4 + 4h(T_1)\), as desired.

Therefore, by structural induction, \(n(T) \geq 4h(T)\) for any full quadtree \(T\).